
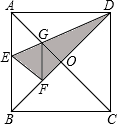
 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G.连接GF,下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G.连接GF,下列结论:分析 ①根据折叠的性质我们能得出∠ADG=∠ODG,也就求出了∠ADG的度数,那么在三角形AGD中用三角形的内角和即可求出∠AGD的度数;
②设AE=x,由△BEF是等腰直角三角形,得出BE=$\sqrt{2}$x,得出AD=AB=x+$\sqrt{2}$x=(1+$\sqrt{2}$)x,由tan∠AED=$\frac{AD}{AE}$,即可求得tan∠AED=$\sqrt{2}+1$;
③设GF=AE=1,由②可知AD=$\sqrt{2}$+1,根据等腰直角三角形的性质求得OD和OF,由△OGD与△FGD同高,根据同高三角形面积的比等于对应底的比,即可求得即可求得S△FGD=$\sqrt{2}$SS△OGD,根据△FGD≌△AGD,得出S△AGD=$\sqrt{2}$S△OGD;
④根据同位角相等得到EF∥AC,GF∥AB,由折叠的性质得出AE=EF,即可判定四边形AEFG是菱形;
⑤通过相似三角形DEF和DOG得出EF和OG的比例关系,然后再在直角三角形BEF中求出BE和EF的关系,进而求出BE和OG的关系.
解答 解:在正方形纸片ABCD中,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,
∴∠GAD=45°,∠ADG=$\frac{1}{2}$∠ADO=22.5°,
∴∠AGD=112.5°,所以①正确.
设AE=x,
∵∠ABD=45°,∠EFD=90°,
∴△BEF是等腰直角三角形,
∴EF=BF=AE=x,
∴BE=$\sqrt{2}$x,
∴AD=AB=x+$\sqrt{2}$x=(1+$\sqrt{2}$)x,
∴tan∠AED=$\frac{AD}{AE}$=$\frac{(1+\sqrt{2})x}{x}$=1+$\sqrt{2}$,所以②正确.
根据题意可得:AE=EF,AG=FG,
∵∠BAC=∠CEF=45°,
∴EF∥AC,
∵∠DAC=∠OFG=45°=∠ABD,
∴GF∥AB,
∴四边形AEFG是菱形,所以④正确.
由∠OFG=45°,AC⊥BD,
∴△GOF是等腰直角三角形,
∴OF=$\frac{\sqrt{2}}{2}$GF,
设GF=AE=1,由②可知AD=$\sqrt{2}$+1,
∴OF=$\frac{\sqrt{2}}{2}$,OD=$\frac{\sqrt{2}}{2}$($\sqrt{2}$+1)=1+$\frac{\sqrt{2}}{2}$,
∴FD=OF+OD=1+$\sqrt{2}$,
因为△OGD与△FGD同高,
∴$\frac{{S}_{△FGD}}{{S}_{△OGD}}$=$\frac{FD}{OD}$=$\frac{1+\sqrt{2}}{1+\frac{\sqrt{2}}{2}}$=$\sqrt{2}$,
∴S△FGD=$\sqrt{2}$SS△OGD,
∵△FGD≌△AGD,
∴S△AGD=$\sqrt{2}$S△OGD,所以③正确;
设BF=EF=AE=FG═AG=1,则OG=$\frac{\sqrt{2}}{2}$,AB=1+$\sqrt{2}$,BD=2+$\sqrt{2}$,DF=1+$\sqrt{2}$,
∵四边形AEFG是菱形,
∴EF∥AG∥AC,
∴△DOG∽△DFE,
∴$\frac{OG}{EF}$=$\frac{DO}{DF}$=$\frac{\sqrt{2}}{2}$,
∴$\sqrt{2}$EF=2OG,
在等腰直角三角形BEF和等腰直角三角形OFG中,BE2=2EF2=2GF2=2×2OG2,
∴BE=2OG.所以⑤正确.
故正确的结论有①②③④⑤.
故答案为①②③④⑤.
点评 本题主要考查了正方形的性质,菱形的判定,相似三角形的判定和性质等知识点,根据折叠的性质的角和边相等是解题的关键.折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.


科目:初中数学 来源: 题型:选择题
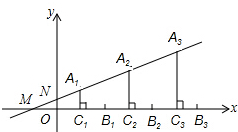 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{30}{x}=\frac{30+15}{x+5}$ | B. | $\frac{30}{x}=\frac{30+15}{x}+5$ | C. | $\frac{30}{x}+5=\frac{30+15}{x}$ | D. | $\frac{30}{x+5}=\frac{30+15}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?
近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )| A. | $\frac{3}{5}$ | B. | $\frac{3\sqrt{13}}{13}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{13}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
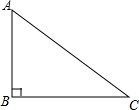 如图,△ABC中,∠ABC=90°.
如图,△ABC中,∠ABC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
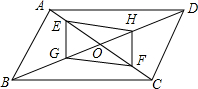 如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.求证:四边形EGFH是平行四边形.
如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.求证:四边形EGFH是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.394×105 | B. | 3.94×104 | C. | 39.4×103 | D. | 4.0×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com