
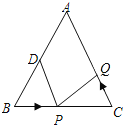
【题目】如图,![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米/秒的速度由
厘米/秒的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.若点
点运动.若点![]() 的运动速度为
的运动速度为![]() 厘米/秒,则当
厘米/秒,则当![]() 与
与![]() 全等时,
全等时,![]() 的值为__________.
的值为__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
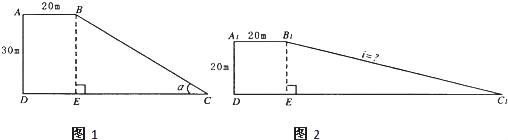
【题目】一段路基的横断面是直角梯形,如图1,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图2的技术要求.试求出改造后坡面的坡度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.

(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
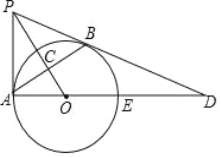
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生最喜爱的一项课外活动项目,随机对全校部分学生进行了一次调査,调査结果有三种情况:A.文学艺术;B.科技制作;C.体育运动.并将调查结果绘制成如下的不完整统计图.
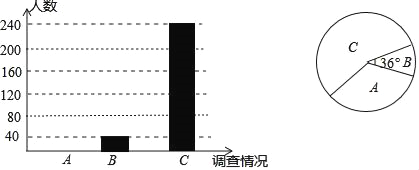
请根据相关信息,解答下列问题:
(1)本次活动共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中A所在扇形的圆心角的度数;
(3)若该校共有1400名学生,试估计该校学生中最喜爱文学艺术的人数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() .
.
下列结论:①![]() ,②
,②![]() ,
,
③当![]() 时,
时,![]() 是等边三角形,
是等边三角形,
④当![]() 时,
时,![]() ,
,
其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的最大值.解决方法:以
的最大值.解决方法:以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,推出
,推出![]() ,当点
,当点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值
取得最大值![]() .
.
问题解决:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() 取得最大值时,
取得最大值时,![]() 的度数为_________.
的度数为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com