
【题目】如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.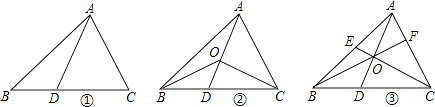
问题引入:
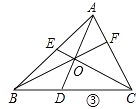
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=;当点D是BC边上任意一点时,S△ABD:S△ABC=(用图中已有线段表示).
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想 ![]() +
+ ![]() +
+ ![]() 的值,并说明理由.
的值,并说明理由.
【答案】
(1)解:1:2;BD:BC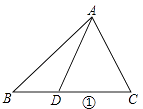
探索研究:
(2)
解:S△BOC:S△ABC=OD:AD,
如图②作OE⊥BC与E,作AF⊥BC与F,
∵OE∥AF,
∴△OED∽△AFD,
![]() .
.
∵ 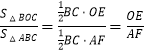 ,
,
∴ ![]()
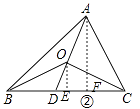
拓展应用:
(3)
解: ![]() +
+ ![]() +
+ ![]() =1,理由如下:
=1,理由如下:
由(2)得 ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]()
= ![]()
= ![]()
=1.
【解析】解:(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=1:2;当点D是BC边上任意一点时,S△ABD:S△ABC=BD:BC,所以答案是:1:2,BD:BC;(1)根据三角形的面积公式,两三角形等高时,可得两三角形底与面积的关系,可得答案;(2)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,可得答案;(3)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,再根据分式的加减,可得答案.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.


科目:初中数学 来源: 题型:
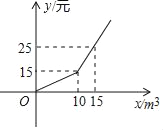
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y元与每月用水量xm3之间的关系如图所示.
(1)求关于x的函数解析式;
(2)若某用户二、三月份共用水22m3(二月份用水量比三月份用水量多),缴纳水费共35元,则该用户二月份的用水量是多少m3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)自2014年12月启动“绿茵行动,青春聚力”郴州共青林植树活动以来,某单位筹集7000元购买了桂花树和樱花树共30棵,其中购买桂花树花费3000元.已知桂花树比樱花树的单价高50%,求樱花树的单价及棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
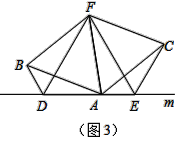
【题目】问题发现:如图,已知:AB=AC,∠BAC=90°,直线m经过点A,过点B作BD⊥m于D, CE⊥m于E.我们把这种常见图形定义为“K”字图.很容易得到线段DE、BD、CE之间的数量关系是 .
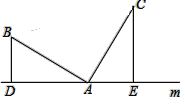
拓展探究:如图2,若AB=AC,∠BAC=∠BDA=∠AEC,则线段DE、BD、CE之间的数量关系还成立吗?如果成立,请证明之.
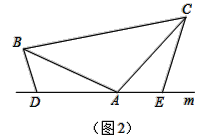
解决问题:如图3,若AB=AC,∠BAC=∠BDA=∠AEC=120°,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,BD=2,CE=4,求△DEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
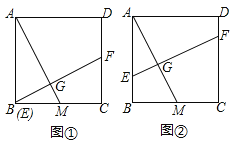
【题目】如图,正方形ABCD,AB=4,点M是边BC的中点,点E是边AB上的一个动点,作EG⊥AM交AM于点G,EG的延长线交线段CD于点F.
(1)如图①,当点E与点B重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD的面积为y,求y与x的函数解析式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为45°的方向上,请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值: ![]() ≈1.7)
≈1.7)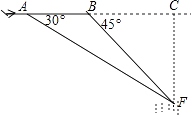
查看答案和解析>>
科目:初中数学 来源: 题型:
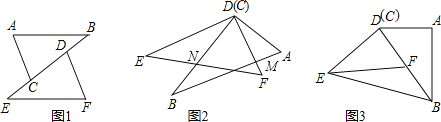
【题目】如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com