
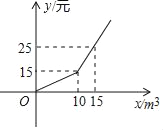
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y元与每月用水量xm3之间的关系如图所示.
(1)求关于x的函数解析式;
(2)若某用户二、三月份共用水22m3(二月份用水量比三月份用水量多),缴纳水费共35元,则该用户二月份的用水量是多少m3?
【答案】(1)y=![]() ;(2)该用户二、三月份的用水量各是8m3、14m3.
;(2)该用户二、三月份的用水量各是8m3、14m3.
【解析】
(1)根据函数图象可以分别设出各段的函数解析式,然后根据函数图象中的数据求出相应的函数解析式;
(2)根据题意对x进行取值进行讨论,从而可以求得该用户二、三月份的用水量各是多少m3.
解:(1)当0≤x≤10时,设y与x的函数关系式为y=kx,
10k=15,得k=1.5,
即当0≤x≤10时,y与x的函数关系式为y=1.5x,
当x>10时,设y与x的函数关系式为y=ax+b,
![]() ,得
,得![]() ,
,
即当x>10时,y与x的函数关系式为y=2x﹣5,
由上可得,y与x的函数关系式为y=![]() ;
;
(2)设二月份的用水量是xm3,
当10<x≤15时,2x﹣5+2(22﹣x)﹣5=35,
解得,x无解,
当0<x≤10时,1.5x+2(22﹣x)﹣5=35,
解得,x=8,
∴22﹣x=14,
答:该用户二、三月份的用水量各是8m3、14m3.


科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.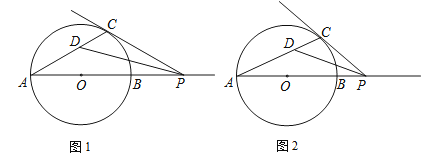
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①-a一定是负数;②|-a|一定是正数;③倒数等于它本身的数是±1;
④绝对值等于它本身的数是1;⑤两个有理数的和一定大于其中每一个加数;⑥若![]() ,则a=b.
,则a=b.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为某校九年级男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1∶2∶5∶6∶4,第四组的频数是12.有下面的4个结论:
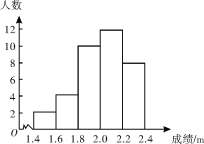
①一共测试了36名男生的成绩;②男子立定跳远成绩的中位数分布在1.8~2.0组;③男子立定跳远成绩的平均数不超过2.2;④如果男子立定跳远成绩低于1.85 m为不合格,那么不合格人数为6人.
其中结论正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
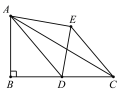
【题目】如图,在Rt△ABC中,AB=3,BC=8,点D为BC的中点,将△ABD沿AD折叠,使点B落在点E处,连接CE,则CE的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.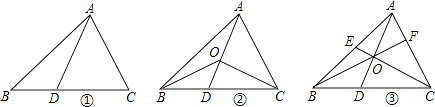
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=;当点D是BC边上任意一点时,S△ABD:S△ABC=(用图中已有线段表示).
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想 ![]() +
+ ![]() +
+ ![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com