
【题目】如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE : EC=4 : 1,则线段DE的长为______.

【答案】![]()
【解析】由矩形ABCD,得∠B=∠C=90,CD=AB,AD=BC,AD∥BC.
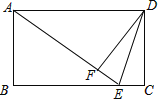
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,
由AD∥BC得∠DAF=∠AEB,
∴在△ABE与△DFA中,
 ,
,
∴△ABE≌△DFA(AAS).
∵由EC:BE=1:4,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=6,
∴x=2,
在Rt△DCE中,DE=![]() =
=![]() =
=![]() .
.
故答案是: ![]() .
.


科目:初中数学 来源: 题型:
【题目】某小区为了促进生活垃圾的分类处理,将生活垃圾分为:可回垃圾、厨余垃圾、其他垃圾三类,分别记为A,B,C:并且设置了相应的垃圾箱,依次记为a,b,c.
(1)若将三类垃圾随机投入三个垃圾箱,请你用树形图的方法求垃圾投放正确的概率:
(2)为了调查小区垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总重500kg生活垃圾,数据如下(单位:)
a | b | c | |
A | 40 | 15 | 10 |
B | 60 | 250 | 40 |
C | 15 | 15 | 55 |
试估计“厨余垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为班级联欢会设计了一个摸球游戏.游戏规则如下:在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.游戏者先从纸箱里随机摸出一个球,记录颜色后放回,将小球摇匀,再随机摸出一个球,若两次摸到的球颜色相同,则游戏者可获得一份纪念品.请你利用树状图或列表法求游戏者获得纪念品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: ①所调查的七年级50名学生在这个月内做好事次数的平均数是 , 众数是 , 极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
【答案】解:①平均数;(2×5+3×6+4×13+5×16+6×10)÷50=4.4;
众数:5次;
极差:6﹣2=4;
②做好事不少于4次的人数:800× ![]() =624;
=624;
(1)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球. ①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?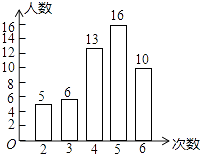
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点B(a,5)在第二象限,点C在y轴上移动,以BC为斜边作等腰直角△BCD,我们发现直角顶点D点随着C点的移动也在一条直线上移动,这条直线的函数表达式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
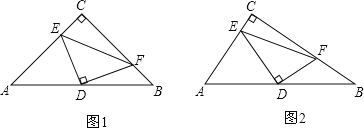
【题目】已知:如图1,Rt△ABC中,∠ACB=90°,D为AB中点,DE、DF分别交AC于E,交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA<CB,(1)中结论还能成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com