
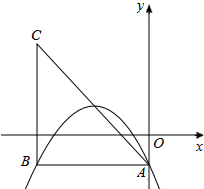
 在平面直角坐标系中,已知抛物线y=ax2-2x+c(a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(-4,3),直角顶点B在第二象限.
在平面直角坐标系中,已知抛物线y=ax2-2x+c(a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(-4,3),直角顶点B在第二象限.分析 (1)根据抛物线对称性得出B点坐标,再根据A、B两点坐标用待定系数法求出抛物线解析式;
(2)求出滑动过程中,抛物线与直线AC的两个交点坐标,利用两点间的距离公式算出PQ为定值;
(3)分两大类情况:
①PQ为直角边,点M到PQ的距离为2$\sqrt{2}$,此时,将直线AC向左平移4个单位后所得直线(y=-x-5)与抛物线的交点,即为所求之M点;
②PQ为斜边,点M到PQ的距离为$\sqrt{2}$.此时,将直线AC向左平移2个单位后所得直线(y=-x-3)与抛物线的交点,即为所求之M点.
解答 解:(1)由题意,得点B的坐标为(-4,-1),
∵抛物线y=ax2-2x+c过A(0,-1),B(-4,-1)两点,
∴$\left\{\begin{array}{l}{c=-1}\\{16a+8+c=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=-1}\end{array}\right.$.
∴抛物线的函数表达式为:$y=-\frac{1}{2}{x}^{2}-2x-1$.
(2)PQ的长度是定值,为$2\sqrt{2}$.
∵A(0,-1),C(-4,3),
∴直线AC的解析式为:y=-x-1.
设平移前抛物线的顶点为P0,则由(1)可得P0的坐标为(-2,1),且P0在AC上.
∵点P在直线AC上滑动,
∴可设P点坐标为(m,-m-1),
则平移后抛物线的函数表达式为:$y=-\frac{1}{2}(x-m)^{2}-m-1$.
解方程组:$\left\{\begin{array}{l}{y=-x-1}\\{y=-\frac{1}{2}(x-m)^{2}-m-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=m}\\{{y}_{1}=-m-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=m+2}\\{{y}_{2}=-m-3}\end{array}\right.$;
∴P(m,-m-1),Q(m+2,-m-3),
∴PQ=$\sqrt{(m-m-2)^{2}+(-m-1+m+3)^{2}}$=$2\sqrt{2}$=AP0.
(3)若△MPQ为等腰直角三角形,则可分为以下两种情况:
①当PQ为直角边时:点M到PQ的距离为$2\sqrt{2}$(即为PQ的长),
由A(0,-1),B(-4,-1),P0(-2,1)可知,△ABP0为等腰直角三角形,且BP0⊥AC,BP0=$2\sqrt{2}$.
如图,过点B作直线l1∥AC,交抛物线$y=-\frac{1}{2}{x}^{2}-2x-1$于点M,则M为符合条件的点.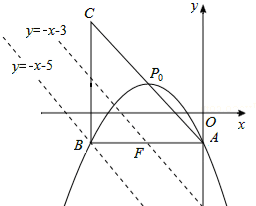 ∴可设直线l1的解析式为:y=-x+b1.
∴可设直线l1的解析式为:y=-x+b1.
∵B(-4,-1),
∴-1=4+b1,
解得:b1=-5,
∴直线l1的解析式为:y=-x-5,
解方程组:$\left\{\begin{array}{l}{y=-x-5}\\{y=-\frac{1}{2}{x}^{2}-2x-1}\end{array}\right.$,
得:$\left\{\begin{array}{l}{{x}_{1}=-4}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-7}\end{array}\right.$,
∴M1(-4,-1),M2(2,-7);
②当PQ为斜边时:MP=MQ=2,可求得点M到PQ的距离为$\sqrt{2}$,
如图,取AB的中点F,则点F的坐标为(-2,-1),
由A(0,-1),F(-2,-1),P0(-2,1)可知:
△AFP0为等腰直角三角形,且点F到直线AC的距离为$\sqrt{2}$,
过点F作直线l2∥AC,交抛物线$y=-\frac{1}{2}{x}^{2}-2x-1$于点M,则M为符合条件的点.
∴可设直线l2的解析式为:y=-x+b2,
∵F(-2,-1),
∴-1=2+b2,
解得b2=-3.
∴直线l2的解析式为:y=-x-3.
解方程组$\left\{\begin{array}{l}{y=-x-3}\\{y=-\frac{1}{2}{x}^{2}-2x-1}\end{array}\right.$,
得:$\left\{\begin{array}{l}{{x}_{1}=-1+\sqrt{5}}\\{{y}_{1}=-2-\sqrt{5}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1-\sqrt{5}}\\{{y}_{2}=-2+\sqrt{5}}\end{array}\right.$.
∴M3($-1+\sqrt{5}$,$-2+\sqrt{5}$),M4($-1-\sqrt{5}$,$-2+\sqrt{5}$).
综上所述,所有符合条件的点M的坐标为:
M1(-4,-1),M2(2,-7),M3($-1+\sqrt{5}$,$-2-\sqrt{5}$),M4($-1-\sqrt{5}$,$-2+\sqrt{5}$).
点评 本题主要考查了二次函数的图象的性质、待定系数法求二次函数和一次函数解析式、平移变换、对称变换、等腰直角三角形的性质、平行四边形的性质、解二元二次方程组、两点间的距离公式等众多知识点,综合性很强,难度很大,是一道经典中考压轴题,要求学生具备扎实的数学功底和熟练的解题技巧.第(3)问的解答体现了分类讨论思想,数形结合思想,动静结合思想,要引起重视.


科目:初中数学 来源: 题型:选择题
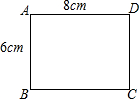 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
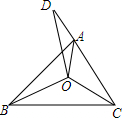 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=92°,则∠BCA的度数为42°.
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=92°,则∠BCA的度数为42°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
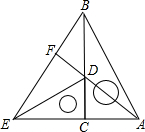 把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.试说明:
把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.试说明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com