
【题目】在数学课上,老师提出如下问题:尺规作图:确定图1中![]() 所在圆的圆心.
所在圆的圆心.
已知:![]() .
.
求作:![]() 所在圆的圆心
所在圆的圆心![]() .
.
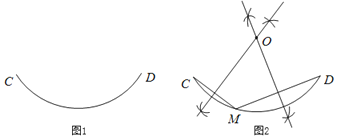
曈曈的作法如下:如图2,
(1)在![]() 上任意取一点
上任意取一点![]() ,分别连接
,分别连接![]() ,
,![]() ;
;
(2)分别作弦![]() ,
,![]() 的垂直平分线,两条垂直平分线交于点
的垂直平分线,两条垂直平分线交于点![]() .点
.点![]() 就是
就是![]() 所在圆的圆心.
所在圆的圆心.
老师说:“曈曈的作法正确.”
请你回答:曈曈的作图依据是_____.
科目:初中数学 来源: 题型:
【题目】如图1,点O为正六边形对角线的交点,机器人置于该正六边形的某顶点处,柱柱同学操控机器人以每秒1个单位长度的速度在图1中给出线段路径上运行,柱柱同学将机器人运行时间设为t秒,机器人到点A的距离设为y,得到函数图象如图2,通过观察函数图象,可以得到下列推断:①该正六边形的边长为1;②当t=3时,机器人一定位于点O;③机器人一定经过点D;④机器人一定经过点E;其中正确的有( )
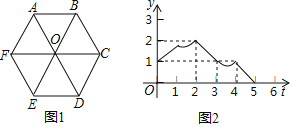
A.①④B.①③C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】明朝的数学家程大位在《算法统宗》中有一道古诗趣题:甲赶群羊逐草茂,乙拽只羊随其后,戏问甲及一百否?甲云所曰无差谬;若得这般一群羊,再添半群小半群,得你一只来方凑,玄机妙算谁猜透?其大意是:甲赶一群羊去放,乙也牵着一只羊跟在甲的后面.乙问甲:“你的这群羊有没有一百只呢?”甲说:“我再得这样的一群羊,再得这群羊的一半,还得这群羊的四分之一,最后凑上你的这只羊,正好是一百只.”问甲原有多少只羊?设甲原有x只羊,根据题意,可列方程为_________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据函数学习中积累的知识与经验,李老师要求学生探究函数y=![]() +1的图象.同学们通过列表、描点、画图象,发现它的图象特征,请你补充完整.
+1的图象.同学们通过列表、描点、画图象,发现它的图象特征,请你补充完整.
(1)函数y=![]() +1的图象可以由我们熟悉的函数 的图象向上平移 个单位得到;
+1的图象可以由我们熟悉的函数 的图象向上平移 个单位得到;
(2)函数y=![]() +1的图象与x轴、y轴交点的情况是: ;
+1的图象与x轴、y轴交点的情况是: ;
(3)请你构造一个函数,使其图象与x轴的交点为(2,0),且与y轴无交点,这个函数表达式可以是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+ax+2a+1的图象经过点M(2,-3)。
(1)求二次函数的表达式;
(2)若一次函数y=kx+b(k≠0)的图象与二次函数y=x2+ax+2a+1的图象经过x轴上同一点,探究实数k,b满足的关系式;
(3)将二次函数y=x2+ax+2a+1的图象向右平移2个单位,若点P(x0,m)和Q(2,n)在平移后的图象上,且m>n,结合图象求x0的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△ADE的周长为( )
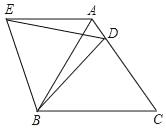
A. 19B. 20C. 27D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
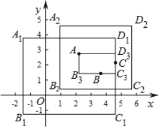
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A(﹣2,3),B(5,0),C(t,﹣2).
①当t=2时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;
(2)已知点D(1,1).E(m,n)是函数y=![]() (x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善寄宿制学校学生的居住条件,某市财政局准备给部分学校加装空调.经市场调研发现:购买1台![]() 种型号的空调和2台
种型号的空调和2台![]() 种型号的空调共需资金6400元;购买2台
种型号的空调共需资金6400元;购买2台![]() 型空调和3台
型空调和3台![]() 型空调共需资金10600元.
型空调共需资金10600元.
(1)求![]() ,
,![]() 两种型号的空调单价各是多少元;
两种型号的空调单价各是多少元;
(2)现计划购进![]() ,
,![]() 两种型号的空调共200台,其中
两种型号的空调共200台,其中![]() 型空调为
型空调为![]() 台,并且要求公司15日内(含15日)完成安装调试.公司承诺:若
台,并且要求公司15日内(含15日)完成安装调试.公司承诺:若![]() 型空调不大于75台,则
型空调不大于75台,则![]() 型空调一定能保证15天内完成安装与调试,同时
型空调一定能保证15天内完成安装与调试,同时![]() 型空调每天可以完成10台的安装与调试;价格方面,当购买
型空调每天可以完成10台的安装与调试;价格方面,当购买![]() 型空调不少于60台时,公司给予
型空调不少于60台时,公司给予![]() 型空调7折优惠;当购买
型空调7折优惠;当购买![]() 型空调大于140台时,公司给予
型空调大于140台时,公司给予![]() 型空调8折优惠.若既能保证如期完成安装调试又能使花费资金最少,应购买
型空调8折优惠.若既能保证如期完成安装调试又能使花费资金最少,应购买![]() ,
,![]() 两种型号的空调各多少台?
两种型号的空调各多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com