
【题目】在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,二次函数y=x2+mx+n的图象经过点A.
(1)当m=4时,求n的值;
(2)设m=﹣2,当﹣3≤x≤0时,求二次函数y=x2+mx+n的最小值;
(3)当﹣3≤x≤0时,若二次函数﹣3≤x≤0时的最小值为﹣4,求m、n的值.
【答案】
(1)解:当y=x+3=0时,x=﹣3,
∴点A的坐标为(﹣3,0).
∵二次函数y=x2+mx+n的图象经过点A,
∴0=9﹣3m+n,即n=3m﹣9,
∴当m=4时,n=3m﹣9=3
(2)解:抛物线的对称轴为直线x=﹣ ![]() ,
,
当m=﹣2时,对称轴为x=1,n=3m﹣9=﹣15,
∴当﹣3≤x≤0时,y随x的增大而减小,
∴当x=0时,二次函数y=x2+mx+n的最小值为﹣15
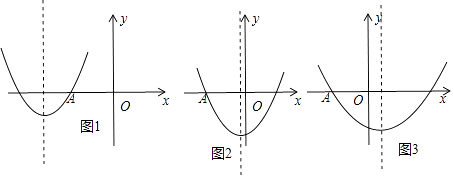
(3)解:①当对称轴﹣ ![]() ≤﹣3,即m≥6时,如图1所示.
≤﹣3,即m≥6时,如图1所示.
在﹣3≤x≤0中,y=x2+mx+n的最小值为0,
∴此情况不合题意;
②当﹣3<﹣ ![]() <0,即0<m<6时,如图2,
<0,即0<m<6时,如图2,
有 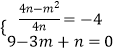 ,
,
解得: ![]() 或
或 ![]() (舍去),
(舍去),
∴m=2、n=﹣3;
③当﹣ ![]() ≥0,即m≤0时,如图3,
≥0,即m≤0时,如图3,
有 ![]() ,
,
解得: 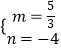 (舍去).
(舍去).
综上所述:m=2,n=﹣3.
【解析】(1)利用一次函数图象上点的坐标特征可求出点A的坐标,再利用二次函数图象上点的坐标特征可得出n=3m﹣9,代入m=4可求出n值;(2)由m=﹣2可求出抛物线对称轴为x=1、n=﹣15,由当﹣3≤x≤0时,y随x的增大而减小,即可得出此时二次函数y=x2+mx+n的最小值;(3)分m≥6、0<m<6和m≤0三种情况,结合二次函数的图象以及y在﹣3≤x≤0时的最小值为﹣4,即可求出m、n的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,求证:DF∥BE

证明:∵DF平分∠ADE(已知)
∴__________=![]() ∠ADE( )
∠ADE( )
∵∠ADE=60°(已知)
∴_________________=30°( )
∵∠1=30°(已知)
∴____________________( )
∴____________________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为8,⊙O经过点C和点D,且与AB相切于点E.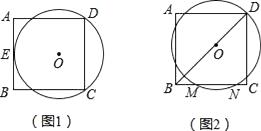
(1)求⊙O的半径;
(2)如图2,平移⊙O,使点O落在BD上,⊙O经过点D,BC与⊙O交于M,N,求MN2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点![]() 在
在![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交线段
交线段![]() 于点
于点![]() .
.

实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现![]() ,
,![]() ,请说明理由;
,请说明理由;
探究应用
(3)缜密小组在勤奋小组探究的基础上,测得![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com