
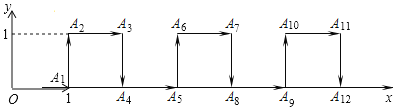
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…第n次移动到An.则△OA6A2020的面积是( )
A.505![]() B.504.5
B.504.5![]() C.505.5
C.505.5![]() D.1010
D.1010![]()
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
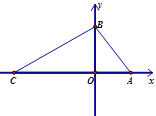
【题目】如图,在平面直角坐标系中,O为坐标原点,A(a,0),B(0,b),且a,b满足![]() ,连接AB,AB=5.C(-7,0)是x轴负半轴上一点,连接BC.
,连接AB,AB=5.C(-7,0)是x轴负半轴上一点,连接BC.
(1)求OA、OB的长;
(2)动点P从点B出发,沿BA以每秒2个单位的速度向终点A匀速运动,连接CP,设点P的运动时间为t,△CBP的面积为S,用含t的代数式表示S(不要求写出t的取值范围)
(3)在(2)的条件下,连接OP,是否存在t值,使S△BCP=![]() S△PCO,如果存在,求出相应的t值,并直接写出P点坐标.若不存在,说明理由.
S△PCO,如果存在,求出相应的t值,并直接写出P点坐标.若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )

A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1. 5倍.设两人出发x min后距出发点的距离为y m.图中折线段OBA表示小明在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).
(1)点B所表示的实际意义是 ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
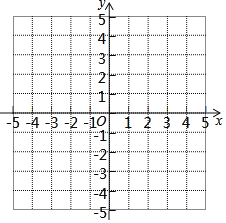
【题目】已知在平面直角坐标系中有三点A(﹣2,1),B(3,1),C(2,3),请解答下列问题:
(1)在坐标系内描出A,B,C的位置;
(2)画出△ABC关于x轴对称的图形△A1B1C1,并写出顶点A1,B1,C1的坐标;
(3)写出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(观察思考):如图,线段AB上有两个点C、D,图中共有 条线段;
![]()
(2)(模型构建):如果线段上有m个点(包括线段的两个端点),则该线段上共有 条线段.请简要说明结论的正确性;
(3)(拓展应用):8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行 场比赛.类比(模型构建)简要说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com