Question

【题目】在的方格纸中，每个小格的顶点叫做格点．以格点连线为边的三角形叫做格点三角形．

请你在图的方格纸中，画一个格点三角形，使与一个格点三角形相似（相似比不为）．

请你在图的方格纸中，画一个格点三角形，使与一个格点三角形相似，面积最大，并求最大值是多少．

与的相似比不是的格点三角形共有几个（相似比相同时只算个）？

Answer 1

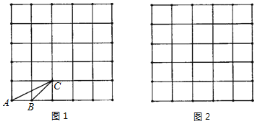
【答案】（1）详见解析；（2）详见解析；（3）4个．

【解析】

（1）根据网格结构，利用三边对应成比例两三角形相似，根据勾股定理作出相似的三角形即可；（2）根据网格结构，在网格中所画三角形的边长最长为，再利用三边对应成比例两三角形相似，根据勾股定理作出相似的三角形即可，利用相似三角形面积的比等于相似比的平方求大三角形的面积即可；（3）根据勾股定理、网格结构及相似三角形的性质，在网格中可以画出边长分别为① ；②；③ ；④、、的三角形，与△ABC相似，故答案为4个.

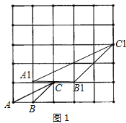
如图所示：

如图所示：

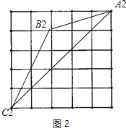
最大格点三角形三边分别为：，，；

根据相似比为：，

∴三角形面积比为：，

∴最大值为：．

根据三角形最大边长以及最小边长即可得出答案：个．