
【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )

A. ①② B. ③④ C. ①③④ D. ①②④
科目:初中数学 来源: 题型:
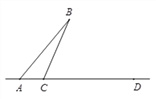
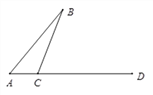
【题目】如图,线段AB,AD交于点A.C为直线AD上一点(不与点A,D重合).过点C在BC的右侧作射线CE⊥BC,过点D作直线DF∥AB,交CE于点G(G与D不重合).
(1)如图1,若点C在线段AD上,且∠BCA为钝角.
①按要求补全图形;②判断∠B与∠CGD的数量关系,并证明.
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系 ;
附加题(2分).
请你结合28题的题意提出一个新的拓展问题 .
查看答案和解析>>
科目:初中数学 来源: 题型:
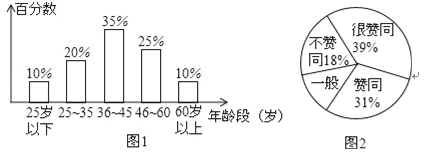
【题目】据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)图2中所缺少的百分数是 ;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是 ____ (填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ___ ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有 ____名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点P是对角线AC上的任意一点(不包括端点),以P为圆心的圆与AB相切,则AD与⊙P的位置关系是( )
A. 相离 B. 相切 C. 相交 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.

(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com