
【题目】如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
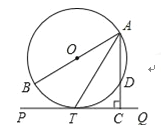
(1)求证:AT平分∠BAC;
(2)若AO=2,AT=![]() ,求AC的长.
,求AC的长.
【答案】(1)AT平分∠BAC;(2)AC=3.
【解析】
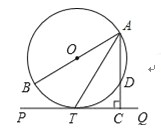
试题分析:(1)连接OT,如图,根据切线的性质得OT⊥PQ,加上AC⊥PQ,则可判断OT∥AC,所以∠TAC=∠OTA,而∠OTA=∠OAT,所以∠TAC=∠OAT;
(2)连接BT,如图,证明Rt△ABT∽Rt△ATC,然后利用相似比克计算出AC的长.
试题解析:(1)证明:连接OT,如图,
∵PQ切⊙O于T,
∴OT⊥PQ,
∵AC⊥PQ,
∴OT∥AC,
∴∠TAC=∠OTA,
而OT=OA,
∴∠OTA=∠OAT,
∴∠TAC=∠OAT,
∴AT平分∠BAC;
(2)连接BT,如图,
∵AB为直径,
∴∠ATB=90°,
∵∠TAC=∠BAT,
∴Rt△ABT∽Rt△ATC,
∴![]() ,即
,即![]() ,
,
∴AC=3.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为4,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
A. 点A在⊙O上 B. 点A在⊙O外
C. 点A在⊙O内 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算中,正确的是( )
A.(﹣a)2(a3)2=﹣a8
B.(﹣a)(﹣a3)2=a7
C.(﹣2a2)3=﹣8a6
D.(ab2)2(a2b)=a3b5
查看答案和解析>>
科目:初中数学 来源: 题型:
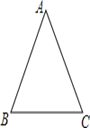
【题目】如图,已知在△ABC中,AB=AC.
(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )

A. ①② B. ③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件商品进价为a元,商店将价格提高30%作零售价销售,在销售旺季过后,商店又以8折的价格开展促销活动.此时这件商品的售价为 ( )
A.a元
B.0.8a元
C.1.04a元
D.0.92a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南北朝著名的数学家祖冲之算出圆周率约为3.1415926,在3.1415926这个数中数字“1”出现的频数与频率分别为( )
A. 2,20% B. 2,25% C. 3,25% D. 1,20%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com