
分析 (Ⅰ)把方程左边进行因式分解得到(x-1)(x+3)=0,再解一元一次方程即可;
(Ⅱ)首先找出a=2,b=-3,c=-$\frac{3}{2}$,然后代入△=b2-4ac,判断根的情况即可.
解答 解:(Ⅰ)解方程 x2+2x-3=0,
因式分解,得(x-1)(x+3)=0,
于是得x-1=0,或x+3=0,
x1=1,x2=-3.
(Ⅱ)解:a=2,b=-3,c=-$\frac{3}{2}$,
∵△=b2-4ac=(-3)2-4×2×(-$\frac{3}{2}$)=9+12=21>0,
∴方程有两个不相等的实数根.
点评 本题主要考查了因式分解法解一元二次方程以及根的判别式的知识,解答本题的关键是熟练掌握因式分解法解一元二次方程的方法步骤,此题难度一般.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
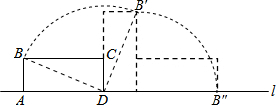 如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线上进行两次旋转,则点B在两次旋转过程中经过的路径的长是$\frac{25}{2}π$.
如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线上进行两次旋转,则点B在两次旋转过程中经过的路径的长是$\frac{25}{2}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<-3 | B. | x>$\frac{3}{2}$ | C. | -3<x<$\frac{3}{2}$ | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com