
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
 已知关于x的一元二次方程x2-(3m+2)x+(2m2+2m-$\frac{1}{2}$)=0.
已知关于x的一元二次方程x2-(3m+2)x+(2m2+2m-$\frac{1}{2}$)=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
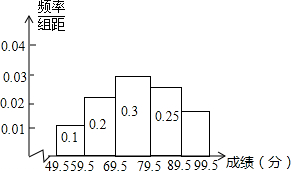 某区有6000名学生参加了“创建国家卫生城市”知识竞赛,为了了解本次竞赛成绩分布情况,竞赛组委会从中随机抽取部分学生的成绩(得分都是整数)作为样本,绘制成频率分布直方图如图,请根据提供的信息估计该区本次竞赛成绩在89.5分-99.5分的学生大约有900名.
某区有6000名学生参加了“创建国家卫生城市”知识竞赛,为了了解本次竞赛成绩分布情况,竞赛组委会从中随机抽取部分学生的成绩(得分都是整数)作为样本,绘制成频率分布直方图如图,请根据提供的信息估计该区本次竞赛成绩在89.5分-99.5分的学生大约有900名.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
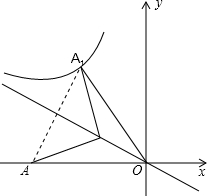 如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )
如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )| A. | -12 | B. | -12$\sqrt{5}$ | C. | -24 | D. | -48 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,$\frac{1}{2}$) | B. | (1,2) | C. | (1,-$\frac{1}{2}$) | D. | (1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com