Question

19．已知关于x的一元二次方程x²-（3m+2）x+（2m²+2m-$\frac{1}{2}$）=0．
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x₁，x₂（其中x₁＜x₂若y是关于m的函数，且y=（x₁-x₂）²，求这个函数的解析式，并写出当-3≤m＜0时，x₂-x₁的取值范围．
（3）在图示坐标系中画出（2）中函数向下平移了3个单位长度后的大致图象，若将该图象在坐标轴y=0下方的部分沿坐标轴y=0翻折，其余部分图象保持不变，得到一个新图象，请你结合这个新图象回答，当直线y=2m+b此新图象有两个公共点时，b的取值范围．

Answer 1

分析 （1）根据根的判别式可得△=（m+2）²+2，由于（m+2）²≥0，进而可判断△＞0，从而可判断此方程有两个不相等的实数根；
（2）根据根与系数的关系得出x₁+x₂=3m+2，x₁，x₂=2m²+2m-$\frac{1}{2}$，再根据y=（x₁-x₂）²=（x₁+x₂）²-4x₁x₂，求出x₂-x₁的值，再根据m的取值范围，即可得出答案；
（3））先求出函数向下平移了3个单位长度后的解析式，再求出y=（m+2）²-1与x轴的交点坐标，当直线y=2m+b经过A点时，当直线y=2m+b经过B点时b的值，求出x轴上方翻折部分的函数解析式，根据y=2m+b与y=-（m+2）²+1只有一个交点，求出b的值，得出直线y=2m+b与新图象有两个公共点，再根据当b＞6时，此时直线y=2m+b与新图象有两个公共点，即可得出答案．

解答 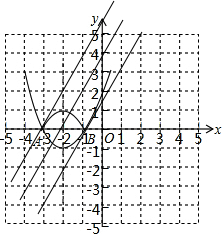解：（1）△=[-（3m+2）]²-4（2m²+2m-$\frac{1}{2}$）=m²+4m+6=（m+2）²+2，
∵（m+2）²≥0，
∴（m+2）²+2＞0，
∴方程有两个不相等的实数根；

（2）∵x₁+x₂=3m+2，x₁，x₂=2m²+2m-$\frac{1}{2}$，
∴y=（x₁-x₂）²=（x₁+x₂）²-4x₁x₂=（3m+2）²-4（2m²+2m-$\frac{1}{2}$）=（m+2）²+2，
∵（x₁-x₂）²=（m+2）²+2，x₁＜x₂，
∴x₂-x₁=$\sqrt{（m+2）^{2}+2}$，
∵当m=0时，x₂-x₁=$\sqrt{6}$，
当m=-3时，x₂-x₁=$\sqrt{3}$，
∴当-3≤m＜0时，x₂-x₁的取值范围是：$\sqrt{3}$≤x₂-x₁＜$\sqrt{6}$；

（3）∵（2）中函数向下平移了3个单位长度后的解析式是：y=（m+2）²-1，
∴设y=（m+2）²-1与x轴的交点坐标x轴交于A、B两点，则A（-3，0），B（-1，0）．
依题意翻折后的图象如图所示．
当直线y=2m+b经过A点时，可得b=2；
当直线y=2m+b经过B点时，可得b=6．
当2＜b＜6时，直线y=2m+b有两个交点，
∵x轴上方翻折部分的函数解析式为：y=-（m+2）²+1，
若y=2m+b与y=-（m+2）²+1只有一个交点，
则方程-（m+2）²+1=2m+b中△=6²-4（b+3）=0，解得b=6，
此时直线y=2m+b与新图象有两个公共点，
当b＞6时，此时直线y=2m+b与新图象有两个公共点；
∴直线y=2m+b此新图象有两个公共点时，b的取值范围是b＞2．

点评 本题考查了根的判别式、根与系数的关系和二次函数的图象和几何变换，关键是根据题意画出图形，注意分三种情况讨论．