
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� ��λ�ù�ϵ�� ��
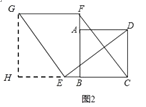
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������жϣ�

���𰸡���1��FG=CE��FG��CE����2����������3��������
��������
�����������1��ֻҪ֤���ı���CDGF��ƽ���ı��μ��ɵó�FG=CE��FG��CE��
��2�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=C��FG��CE��
��3��֤����CBF�ա�DCE����֤���ı���CEGF��ƽ���ı��Σ�
�����������1��FG=CE��FG��CE��
��2������G��GH��CB���ӳ����ڵ�H����EG��DE�����GEH+��DEC=90�㣬�ߡ�GEH+��HGE=90�㣬���DEC=��HGE���ڡ�HGE���CED�У��ߡ�GHE=��DCE����HGE=��DEC��EG=DE�����HGE�ա�CED��AAS������GH=CE��HE=CD����CE=BF����GH=BF����GH��BF�����ı���GHBF�Ǿ��Σ���GF=BH��FG��CH����FG��CE�����ı���ABCD�������Σ���CD=BC����HE=BC����HE+EB=BC+EB����BH=EC����FG=EC��
��3�����ı���ABCD�������Σ���BC=CD����FBC=��ECD=90�㣬�ڡ�CBF���DCE�У���BF=CE����FBC=��ECD��BC=DC�����CBF�ա�DCE��SAS�������BCF=��CDE��CF=DE����EG=DE����CF=EG����DE��EG�����DEC+��CEG=90�����ߡ�CDE+��DEC=90�������CDE=��CEG�����BCF=��CEG����CF��EG�����ı���CEGFƽ���ı��Σ���FG��CE��FG=CE��


 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������룺
��1����ͼ�٣��ڡ�ABC�У���O�ǡ�ABC�͡�ACBƽ���ߵĽ��㣬����A=�������BOC= ���æ���ʾ������ͼ�ڣ���CBO=![]() ��ABC����BCO=
��ABC����BCO=![]() ��ACB����A=�������BOC= ���æ���ʾ��
��ACB����A=�������BOC= ���æ���ʾ��
��չ�о���
��2����ͼ�ۣ���CBO=![]() ��DBC����BCO=
��DBC����BCO=![]() ��ECB����A=����������BOC= ���æ���ʾ������˵�����ɣ�
��ECB����A=����������BOC= ���æ���ʾ������˵�����ɣ�
������
��3��BO��CO�ֱ��ǡ�ABC����ǡ�DBC����ECB��n�ȷ��ߣ����ǽ��ڵ�O����CBO=![]() ��DBC����BCO=
��DBC����BCO=![]() ��ECB����A=����������BOC= ��
��ECB����A=����������BOC= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У��������Ǽ�������ǣ� ��
A. ���������ε�������� B. ȫ�������ε������Ӧ�߷ֱ����
C. ��a=b����a2=b2 D. ��a2>b2����|a|>|b|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BC��AC����E��BC�ϣ�CE=CA����D��AB�ϣ�����DE����ACB+��ADE=180�㣬��CH��AB������ΪH��
��1����ͼa������ACB=90��ʱ������CD������C��CF��CD��BA���ӳ����ڵ�F��
����֤��FA=DE��
������������߶�DE��AD��CH֮���������ϵ��ֱ��д�����ۣ�
��2����ͼb������ACB=120��ʱ�������߶�DE��AD��CH֮�����������������ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʽx2ym+2��xny�ĺ���Ȼ��һ������ʽ����(m+n)2019����( )
A. 1 B. ��1 C. 2019 D. ��2019
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD= ![]() AB=
AB= ![]() CD �� �߶�AB��CD���е�E �� F֮�������10cm �� ��AB �� CD�ij���
CD �� �߶�AB��CD���е�E �� F֮�������10cm �� ��AB �� CD�ij���![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com