
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,且DG平分△ABC的周长,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△GBD ∽△GDF,求证:BG⊥CG.

(1)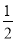 (b+c);(2)证明见解析;(3)证明见解析.
(b+c);(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)由△BDG与四边形ACDG的周长相等与BD=CD,易得BG=AC+AG,即可得BG=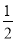 (AB+AC);
(AB+AC);
(2)由点D、F分别是BC、AB的中点,利用三角形中位线的性质,易得DF=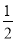 AC=
AC=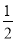 b,由FG=BG-BF,求得DF=FG,又由DE∥AB,即可求得∠FDG=∠EDG;
b,由FG=BG-BF,求得DF=FG,又由DE∥AB,即可求得∠FDG=∠EDG;
(3)由△BDG与△DFG相似,∠DFG>∠B,∠BGD=∠DGF(公共角),可得∠B=∠FDG,又由(2)得:∠FGD=∠FDG,易证得DG=BD=CD,可得B、G、C三点在以BC为直径的圆周上,由圆周角定理,即可得BG⊥CG.
试题解析:(1)【解析】
∵△BDG与四边形ACDG的周长相等,
∴BD+BG+DG=AC+CD+DG+AG,
∵D是BC的中点,
∴BD=CD,
∴BG=AC+AG,
∵BG+(AC+AG)=AB+AC,
∴BG=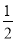 (AB+AC)=
(AB+AC)=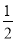 (b+c);
(b+c);
(2)证明:∵点D、F分别是BC、AB的中点,
∴DF=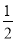 AC=
AC=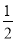 b,BF=
b,BF=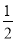 AB=
AB=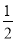 c,
c,
又∵FG=BG-BF=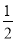 (b+c)-
(b+c)-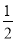 c=
c=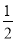 b,
b,
∴DF=FG,
∴∠FDG=∠FGD,
∵点D、E分别是BC、AC的中点,
∴DE∥AB,
∴∠EDG=∠FGD,
∴∠FDG=∠EDG,
即DG平分∠EDF;
(3)证明:∵△BDG与△DFG相似,∠DFG>∠B,∠BGD=∠DGF(公共角),
∴∠B=∠FDG,
由(2)得:∠FGD=∠FDG,
∴∠FGD=∠B,
∴DG=BD,
∵BD=CD,
∴DG=BD=CD,
∴B、G、C三点在以BC为直径的圆周上,
∴∠BGC=90°,
即BG⊥CG.
考点:1.相似三角形的判定与性质;2.三角形中位线定理.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:填空题
如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按逆时针方向旋转90°,则点B的对应点的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:选择题
已知x2-y2=14,x-y=2,则x+y等于
A.6 B.7 C.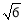 D.
D.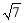
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:选择题
如图所示的几何体中,俯视图形状相同的是( )

A.①④ B.②④ C.①②④ D.②③④
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:解答题
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级新课结束考试数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
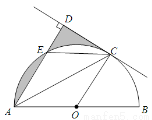
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为1,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:填空题
近年来,我国大部分地区饱受“四面霾伏”的困扰,霾的主要成分是PM2.5,是指直径小于等于0.0000025 m的粒子,数0.0000025用科学记数法可表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com