
分析 (1)紧紧围绕“当每吨售价每下降10元时,月销售量就会增加5吨”列代数式就可以得出结论,
(2)由售价是x元,降价为(260-x),所以销售量是增加7.5×$\frac{260-x}{10}$吨,那么售出的金额是x[($\frac{260-x}{10}$×7.5)+45],根据利润=每件的利润×销售额,可以求出函数的解析式.
(3)由(2)的结论转化为顶点式就可以求出售价和利润的最大值.
解答 解:(1)由题意,得
45+7.5×$\frac{260-220}{10}$=75;
答:当每吨售价是220元时,此时的月销售量是75吨;
(2)由题意,得
y=(x-100)(45+$\frac{260-x}{10}$×7.5),
y=-$\frac{3}{4}$x2+315x-24000;
(3)∵y=-$\frac{3}{4}$x2+315x-24000;
∴y=-$\frac{3}{4}$(x-210)2+9075,
∴当x=210时,y最大=9075,
答:每吨材料售价定为210元时,该经销店获得的月利润最大.,
点评 本题考查了把实际问题转化为二次函数,再对二次函数进行实际应用.此题为数学建模题,借助二次函数解决实际问题.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
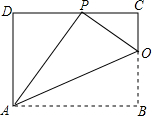 已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
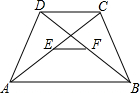 如图:AB∥CD,E,F分别是AC,DB的中点.
如图:AB∥CD,E,F分别是AC,DB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com