
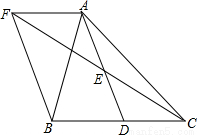
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)试判断线段BD与CD的大小关系;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)若△ABC为直角三角形,且∠BAC=90°时,判断四边形AFBD的形状,并说明理由.
(1)BD=CD;(2)矩形;(3)菱形
【解析】试题分析:(1)根据平行线的性质可得∠FAE=∠CDE,再结合∠AEF=∠DEC,AE=DE,即可证得△AEF≌△DEF,从而可以证得结论;
(2)由AF∥BC,AF=BD可证得四边形AFBD是平行四边形,再根据等腰三角形的性质可得AD⊥BC,即可证得四边形AFBD是矩形;
(3)先根据直角三角形斜边的中线是斜边的一半可证得BD=AD,再结合四边形AFBD是平行四边形可证得四边形AFBD是菱形.
(1)∵AF∥BC,
∴∠FAE=∠CDE,
∵∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEF,
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴四边形AFBD是矩形;
(3)∵∠BAC=90°,BD=CD,
∴BD=AD(直角三角形斜边的中线是斜边的一半).
∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.
本题涉及了平行线的性质,全等三角形的判定和性质,平行四边形、矩形、菱形的判定和性质,特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


科目:初中数学 来源:名师精选(解析版)8 题型:解答题
有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.

(1)用画树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率.
查看答案和解析>>
科目:初中数学 来源:名师精选(解析版)8 题型:选择题
已知圆锥的底面半径为2cm,母线长为6cm,则圆锥的侧面积是( )
A.24cm2 B. cm2 C.12cm2 D.
cm2 C.12cm2 D.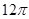 cm2
cm2
查看答案和解析>>
科目:初中数学 来源:名师精选(解析版)5 题型:解答题
已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
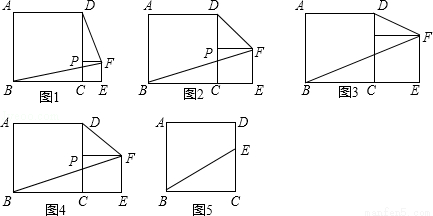
观察计算:
(1)如图1,当a=4,b=1时,四边形ABFD的面积为 _________
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 _________ ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 _________ ;
探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;
(5)综合应用:农民赵大伯有一块正方形的土地(如图5),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com