
已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
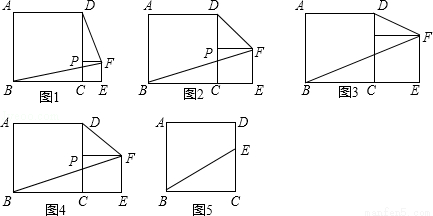
观察计算:
(1)如图1,当a=4,b=1时,四边形ABFD的面积为 _________
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 _________ ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 _________ ;
探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;
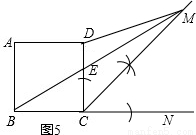
(5)综合应用:农民赵大伯有一块正方形的土地(如图5),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.
16 16 16 相等与正方形PCEF的边长无关
【解析】试题分析:
(1)4×4+(1+4)×1÷2-1×5÷2=16;
(2)4×4+(2+4)×2÷2-2×6÷2=16;
(3)4×4+(3+4)×3÷2-3×7÷2=16;
(4)无论点P在CD边上的什么位置,四边形ABFD的面积与正方形ABCD的面积相等,与正方形PCEF的边长无关.
证明:连接BD,CF,

∵四边形ABCD是正方形,
∴∠DBC=45°,
同理∠FCE=45°,
∴BD∥CF,
∴S△BCD=S△BDF,
∴四边形ABFD的面积与正方形ABCD的面积相等;
(5)如图5,作BC的延长线CN,作∠DCN的角平分线交BE的延长线于点M,则四边形ABMD的面积与正方形ABCD的面积相等,点M即为所求.
考点:1等底等高三角形面积相等;2尺规作图。


科目:初中数学 来源:名师精选(解析版)8 题型:解答题
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
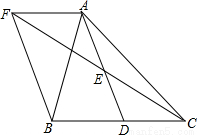
(1)试判断线段BD与CD的大小关系;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)若△ABC为直角三角形,且∠BAC=90°时,判断四边形AFBD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:名师精选(解析版)6 题型:解答题
某校初四年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.

查看答案和解析>>
科目:初中数学 来源:名师精选(解析版)4 题型:填空题
某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示:
移植总数(n) | 400 | 750 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数(m) | 369 | 622 | 1335 | 3203 | 6335 | 8073 | 12628 |
成活的频率 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.897 | 0.902 |
根据表中数据,估计这种幼树移植成活率的概率为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源:名师精选(解析版)3 题型:选择题
如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )
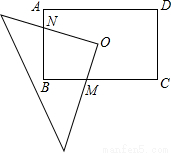
A.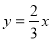 B.
B.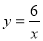 C.y=x D.
C.y=x D.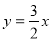
查看答案和解析>>
科目:初中数学 来源:2016届重庆市合川区第五学区七年级下学期半期考试数学试卷(解析版) 题型:解答题
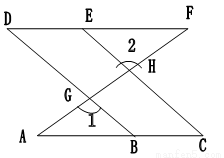
已知:如图, AC∥DF,直线AF分别与直线BD、CE 相交于点G、H,∠1=∠2,
求证: ∠C=∠D.
【解析】
∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=__ _______( 等量代换 )
∴ // ___________( 同位角相等,两直线平行 )
∴∠C=_ _( 两直线平行,同位角相等 )
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com