
【题目】已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.

【答案】(1)y=x2﹣2x﹣3;(2)当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣![]() ,2
,2![]() ),点B的坐标为(
),点B的坐标为(![]() ,﹣2
,﹣2![]() ).(3)不存在,理由详见解析.
).(3)不存在,理由详见解析.
【解析】
试题(1)令x=0求出y值即可得出C点的坐标,又有点(﹣1,0)、(3,0),利用待定系数法求抛物线的解析式即可;(2)将正比例函数解析式代入抛物线解析式中,找出关于x的一元二次方程,根据根与系数的关系即可得出“xA+xB=2+k,xAxB=﹣3”,结合点O为线段AB的中点即可得出xA+xB=2+k=0,由此得出k的值,将k的值代入一元二次方程中求出xA、xB,在代入一次函数解析式中即可得出点A、B的坐标;(3)假设存在,利用三角形的面积公式以及(2)中得到的“xA+xB=2+k,xAxB=﹣3”,即可得出关于k的一元二次方程,结合方程无解即可得出假设不成立,从而得出不存在满足题意的k值.
试题解析:(1)令抛物线y=ax2+bx﹣3中x=0,则y=﹣3,
∴点C的坐标为(0,﹣3).
∵抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,
∴有![]() ,解得:
,解得:![]() ,
,
∴此抛物线的解析式为y=x2﹣2x﹣3.
(2)将y=kx代入y=x2﹣2x﹣3中得:kx=x2﹣2x﹣3,
整理得:x2﹣(2+k)x﹣3=0,
∴xA+xB=2+k,xAxB=﹣3.
∵原点O为线段AB的中点,
∴xA+xB=2+k=0,
解得:k=﹣2.
当k=﹣2时,x2﹣(2+k)x﹣3=x2﹣3=0,
解得:xA=﹣![]() ,xB=
,xB=![]() .
.
∴yA=﹣2xA=2![]() ,yB=﹣2xB=2
,yB=﹣2xB=2![]() .
.
故当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣![]() ,2
,2![]() ),点B的坐标为(
),点B的坐标为(![]() ,﹣2
,﹣2![]() ).
).
(3)假设存在.
由(2)可知:xA+xB=2+k,xAxB=﹣3,
S△ABC=![]() OC|xA﹣xB|=
OC|xA﹣xB|=![]() ×3×
×3×![]() =
=![]() ,
,
∴(2+k)2﹣4×(﹣3)=10,即(2+k)2+2=0.
∵(2+k)2非负,无解.
故假设不成立.
所以不存在实数k使得△ABC的面积为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】(1)已知y=(m2+m)![]() +(m﹣3)x+m2是x的二次函数,求出它的解析式.
+(m﹣3)x+m2是x的二次函数,求出它的解析式.
(2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OC=6,D为半径OC上异于O,C的点,过点D作AB⊥OC,交⊙O于A,B,点E在线段AB上,AE=CE,点P在线段EC的延长线上,PB=PE.
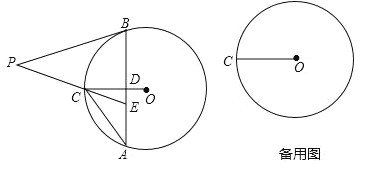
(1)若OD=2,求弦AB的长;
(2)当点D在线段OC(不含端点)上移动时,直线PB与⊙O有怎样的位置关系?请说明理由;
(3)点Q是⊙O上的一个动点,若点D为OC中点时,线段PQ的最小值为多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梧桐山是深圳最高的山峰,某校综合实践活动小组要测量“主山峰”的高度,先在梧桐山对面广场的A处测得“峰顶”C的仰角为45o , 此时,他们刚好与峰底D在同一水平线上。然后沿着坡度为30o的斜坡正对着“主山峰”前行700米,到达B处,再测得“峰顶”C的仰角为60o , 如图,根据以上条件求出“主山峰”的高度?(测角仪的高度忽略不计,结果精确到1米.参考数据:(![]() 1.4,
1.4,![]() 1.7)
1.7)
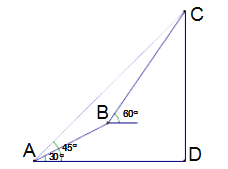
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程两实数根和为﹣4的是( )
A. x2+2x﹣4=0 B. x2﹣4x+4=0 C. x2+4x+10=0 D. x2+4x﹣5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴.上有两个长方形![]() 和
和![]() ,这两个长方形的宽都是
,这两个长方形的宽都是![]() 个单位长度,长方形
个单位长度,长方形![]() 的长
的长![]() 是
是![]() 个单位长度,长方形
个单位长度,长方形![]() 的长
的长![]() 是
是![]() 个单位长度,点
个单位长度,点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且
,且![]() 两点之间的距离为
两点之间的距离为![]() .
.
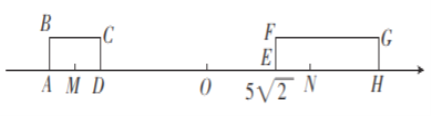
![]() 点
点![]() 在数轴上表示的数是 ,点
在数轴上表示的数是 ,点![]() 在数轴上表示的数是
在数轴上表示的数是
![]() 若线段
若线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 上有一点
上有一点![]() 以每秒
以每秒![]() 个单位长度的速度向右匀速运动,
个单位长度的速度向右匀速运动,![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,设运动的时间为
个单位长度的速度向左运动,设运动的时间为![]() 秒,问当
秒,问当![]() 为多少时,原点
为多少时,原点![]() 恰为线段
恰为线段![]() 的三等分点?
的三等分点?
![]() 若线段
若线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 上有一点
上有一点![]() ,长方形
,长方形![]() 以每秒
以每秒![]() 个单位长度的速度向右匀速运动,长方形
个单位长度的速度向右匀速运动,长方形![]() 保持不动,设运动时间为
保持不动,设运动时间为![]() 秒,是否存在一个
秒,是否存在一个![]() 的值,使以
的值,使以![]() 三点为顶点的三角形是直角三角形?若存在,求
三点为顶点的三角形是直角三角形?若存在,求![]() 的值;不存在,请说明理由.
的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
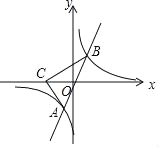
【题目】如图,直线y=3x与双曲线y=![]() 相交于点A,B,点C的坐标是(-4,0),且AO=AC.
相交于点A,B,点C的坐标是(-4,0),且AO=AC.
(1)求双曲线的解析式.
(2)已知A、B两点关于原点对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
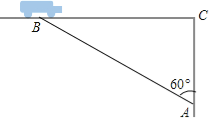
(1)求B、C两点间的距离.
(2)请判断此车是否超过了BC路段限速40千米/小时的速度.(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com