
Àƒäãá¢À¢öÁëˋè§òúèŸÜÖ柡Ôçáè§ñÍȘá°ÅÈæܤüò祪£ŸÑ₤ÅÀæÕ؈ýãê¢À¯ø¼è§ñÍÀÝçá¡ÔÑàȘüàåÖöÁëˋè§Ñåû̿аÀçáAÇÎýãçûÀ¯ñÍÑËÀÝCçáî—§úöˆ45o Ș ÇùòÝȘù«ûú¡í¤ûÆŠñÍçæDåÖë˜Ø£ùÛó§üÔèüÀÈࣤµîÄæéóôÑàöˆ30oçáÅÝóôí»ÑåæéÀ¯ø¼è§ñÍÀÝú¯ÅÅ700ûæȘç§ÇÿBÇÎȘåìýãçûÀ¯ñÍÑËÀÝCçáî—§úöˆ60o Ș àÓë¥È˜¡ªƒïØåèüä¾¥±úµ°—À¯ø¼è§ñÍÀÝçá¡ÔÑàȢȴýã§úØúçá¡ÔÑगôåý£¥óȘ§Ã¿«ƒ¨àñç§1ûæÈÛýö¢¥ò»ƒïȤȴ![]() 1.4Ș
1.4Ș![]() 1.7Èˋ
1.7Èˋ
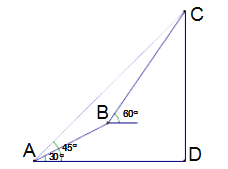
ÀƒÇÞ¯¡À¢À¯Ø£šáüÐÀÝçá¡ÔÑàå¥öˆ150ûæÈÛ
Àƒ§ãö—À¢
òæüà¿»çÐBæ¼BFÀëDCÆÖçÐFȘ¿»çÐBæ¼BEÀëADÆÖçÐEȘ¢èçûùáÝÔÅöBEDFòúƒÄÅöȘࣤµåÖRtÀ¼ABEøÅȘÆè໧ú¤₤ò»çáÅåøòȘ¢èúµçûAEÆŠBEçá°ÊȘåìèÒBF=xûæȘâ«Æû໧ú¤₤ò»çáøˆòѥǢèúµçûñ§°ä55![]() +x=
+x=![]() x+55Ș¥äѽ¢èúµçûÇÞ¯¡ÈÛ
x+55Ș¥äѽ¢èúµçûÇÞ¯¡ÈÛ
¿»çÐBæ¼BFÀëDNÆÖçÐFȘ¿»çÐBæ¼BEÀëADÆÖçÐEȘ

ÀÔÀüD=90ÀÐȘ
ÀÁùáÝÔÅöBEDFòúƒÄÅöȘ
ÀÁBE=DFȘBF=DEȘ
åÖRtÀ¼ABEøÅȘAE=ABcos30ÀÐ=110Àê![]() =55
=55![]() È´ûæÈˋȘBE=ABsin30ÀÐ=
È´ûæÈˋȘBE=ABsin30ÀÐ=![]() Àê110=55È´ûæÈˋÈ£
Àê110=55È´ûæÈˋÈ£
èÒBF=xûæȘå·AD=AE+ED=(55![]() +x)È´ûæÈˋȘ
+x)È´ûæÈˋȘ
åÖRtÀ¼BFNøÅȘCF=BFtan60ÀÐ=![]() xÈ´ûæÈˋȘ
xÈ´ûæÈˋȘ
ÀÁDC=DF+CF=(55+![]() x)È´ûæÈˋȘ
x)È´ûæÈˋȘ
ÀÔÀüCAD=45ÀÐȘ
ÀÁAD=DNȘ
¥Ç55![]() +x=
+x=![]() x+55Ș
x+55Ș
§ãçûȤx=55Ș
ÀÁDN=55+![]() xÀø150È´ûæÈˋÈÛ
xÀø150È´ûæÈˋÈÛ
ÇÞȤÀ¯Ø£šáüÐÀÝçá¡ÔÑàå¥öˆ150ûæÈÛ


 û«ÅÈ¢öäûüçêÅÇÞ¯¡
û«ÅÈ¢öäûüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢çàî■໧úÅöØ£ä¾ÝÔçáÝÔ°Êöˆ3Șù■çáêÚê§ä¾ÝÔçáÝÔ°Êòú¿ÄÆÖxçáØ£åˆÑ±Çöñ§°äx2ˋ12x+k=0çáꧡ—¡ªÈ˜å·kçáøçòú________ÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢üôêÅ¥¡¤öäÍòúÆè4¡—üÁë˜çáÅÀí»ñ§äÍÇŸ°èçáȘóðøÅø¼òÆ륤ëæµòÆë¥üÁë˜çáòúÈ´ÀÀÀÀÈˋ
A.  B.
B. 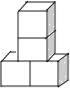
C. 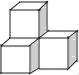 D.
D. 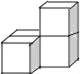
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
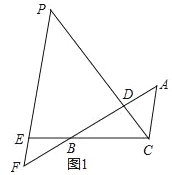
Àƒäãá¢À¢àÓë¥1ȘÀ¼ABCøÅȘçÐDåÖüÔÑöABèüȘçÐEåÖüÔÑöCBîÆ°ÊüÔèüȘúØBE=CDȘEPÀöAC§£øÝüÔCDÆÖçÐPȘ§£øÝüÔABÆÖçÐFȘÀüADP=ÀüACBÈÛ
È´1Èˋë¥1øÅòúñþÇÌåÖÆŠACüÁçàçáüÔÑöÈ¢à¶ÇÌåÖȘúŠíØ°—ȘýÂ¥ÆØåøÊû¼È˜à¶ý£ÇÌåÖȘùçû¼âÚÆèÈ£
È´2Èˋට¨À¯çÐDåÖüÔÑöABèüȘçÐEåÖüÔÑöCBîÆ°ÊüÔèüÀÝ¡áöˆÀ¯çÐDåÖüÔÑöBAîÆ°ÊüÔèüȘçÐEåÖüÔÑöBCîÆ°ÊüÔèüÀÝȘóðù«ä¾¥±ý£ÝðÈ´àÓë¥2ÈˋÈÛçÝÀüABC=90ÀÐȘÀüBAC=60ÀÐȘAB=2òÝȘúµüÔÑöPEçá°ÊÈÛ

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢È´Ýƒäã10ñøÈˋàÓë¥È˜åÖÀ¼ABCøÅȘAB=ACȘØåACöˆø݃Ñæ¼ÀîO§£BCÆÖçÐDȘ¿»çÐDæ¼ÀîOçáúÅüÔȘ§£ABÆÖçÐEȘ§£CAçáîÆ°ÊüÔÆÖçÐFÈÛ
È´1ÈˋúµøÊȤFEÀëABÈ£
È´2ÈˋçÝEF=6Ș![]() =
=![]() òÝȘúµDEçá°ÊÈÛ
òÝȘúµDEçá°ÊÈÛ

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
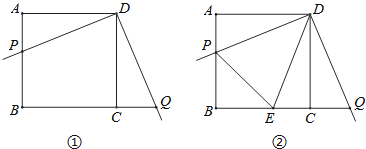
Àƒäãá¢À¢á°ÅÈò»îÏÅùàÊÅÀæÕ¢ˆí¿êùØ£Çö¢öë㣟Ñ₤Ș¿»°äàÓüôȤàÓë¥ÂìȘí»ñ§ÅöABCDøÅȘAB=4Ș§¨à»§ú¯ÍñéåÖí»ñ§ÅöABCDèüȘò¿à»§ú¯ÍçáøݧúÑËçÐÆŠDçÐøĤüÈÛ໧ú¯ÍçáØ£ÝÔ§£ABÆÖçÐPȘêÚØ£ÝÔ§£BCçáîÆ°ÊüÔÆÖçÐQÈÛ
È´1ÈˋúµøÊȤAP=CQÈ£
È´2ÈˋàÓë¥ÂÖȘÅÀû¼åÖë¥1çᣪÇÀèüæ¼ÀüPDQçáó§ñøüÔDE§£BCÆÖçÐEȘ꘧ÆPEȘù«ñÂüøPE¤ëQEÇÌåÖأѴçáò»ê¢¿ÄüçȘúŠýôýãù«çá§ÃôÜýÂÆÒØåøÊû¼È£
È´3ÈˋåÖÈ´2Èˋçáä¾¥±üôȘà¶AP=1ȘúµPEçá°ÊÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢ØîøˆéæöÿüÔyȧax2ȨbxÈÙ3ƒÙ¿»(ÈÙ1Ș0)Ș(3Ș0)ê§çÐȘƊyøç£ÆÖçÐCȘøÝüÔyȧkxÆŠéæöÿüÔ§£ÆÖAȘBê§çÐÈÛ
(1)ÅÇ°—çÐCçáæ½ÝõýÂúµ°—ÇùéæöÿüÔçá§ãö—ò§È£
(2)çÝåÙçÐOöˆüÔÑöABçáøÅçÐòÝȘúµkçáø祯AȘBê§çÐçáæ½ÝõÈ£
(3)òúñþÇÌåÖòçò»kò¿çûÀ¼ABCçáûÌ£»öˆ![]() È¢à¶ÇÌåÖȘúµ°—kçáøçÈ£à¶ý£ÇÌåÖȘúŠùçû¼âÚÆèÈÛ
È¢à¶ÇÌåÖȘúµ°—kçáøçÈ£à¶ý£ÇÌåÖȘúŠùçû¼âÚÆèÈÛ

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜MNòú¯ŠƒÑöˆ2çáÀîOçáø݃ÑȘçÐAåÖÀîOèüȘÀüAMNȧ30ÀÐȘçÐBöˆêÆ£ÀANçáøÅçÐÈÛçÐPòúø݃ÑMNèüØ£Ñ₤çÐȘå·PAȨPBçáæŸÅÀøçöˆ(ÀÀ )
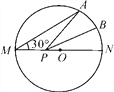
A. 4![]() B. 2 C. 4 D. 2
B. 2 C. 4 D. 2![]()
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜EÀÂFñøÝÞòú ùáÝÔÅöABCDçáÝÔABÀÂCDèüçáçÐȘAFÆŠDEüÁ§£ÆÖçÐPȘBFÆŠCEüÁ§£ÆÖçÐQȘ¥úS1ȧSÀ¼APDȘS2ȧSÀ¼BQCȘùáÝÔÅöEQFPçáûÌ£»öˆSÈÛ
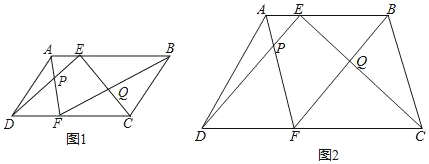
È´1Èˋà¶ùáÝÔÅöABCDöˆó§ÅÅùáÝÔÅöȘàÓë¥1ȘúµøÊȤSȧS1+S2È£
È´2Èˋà¶ùáÝÔÅöABCDöˆØ£¯Ðë¿ÑÁÝÔÅöȘABÀöCDȘàÓë¥2ȘúµøÊȤSȧS1+S2ÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¿º¥òîÏÅÈÆéîÀ - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com