
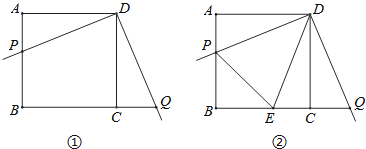
【题目】某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.
【答案】(1)证明见解析;
(2)PE=QE,理由见解析;
(3)PE的长为3.4.
【解析】试题分析:(1)、根据正方形的性质得出∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4,结合∠PDQ=90°得出∠ADP=∠CDQ,从而说明△APD和△CQD全等,从而得出答案;(2)、根据全等得出PD=QD,根据DE为角平分线得出∠PDE=∠QDE,从而说明△PDE和△QDE全等,得出答案;(3)、根据(2)得出PE=QE,根据(1)得出CQ=AP=1。从而得到BQ=5,BP=3,设PE=QE=x,然后利用Rt△BPE的勾股定理得出x的值,得出答案.
试题解析:(1)∵四边形ABCD是正方形,
∴∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4, ∵∠PDQ=90°,
∴∠ADP=∠CDQ,
在△APD和△CQD中, ∴△APD≌△CQD(ASA), ∴AP=CQ;
∴△APD≌△CQD(ASA), ∴AP=CQ;
(2)PE=QE,
理由如下:由(1)得:△APD≌△CQD, ∴PD=QD, ∵DE平分∠PDQ,∴∠PDE=∠QDE,
在△PDE和△QDE中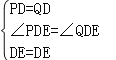 ∴△PDE≌△QDE(SAS), ∴PE=QE;
∴△PDE≌△QDE(SAS), ∴PE=QE;
(3)由(2)得:PE=QE,由(1)得:CQ=AP=1, ∴BQ=BC+CQ=5,BP=AB﹣AP=3,
设PE=QE=x,则BE=5﹣x, 在Rt△BPE中,由勾股定理得:32+(5﹣x)2=x2,
解得:x=3.4, 即PE的长为3.4.


科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
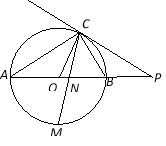
(1)求证:PC是⊙O的切线;
(2)求证:BC=AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
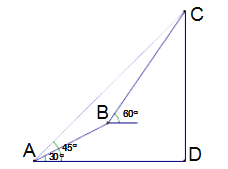
【题目】梧桐山是深圳最高的山峰,某校综合实践活动小组要测量“主山峰”的高度,先在梧桐山对面广场的A处测得“峰顶”C的仰角为45o , 此时,他们刚好与峰底D在同一水平线上。然后沿着坡度为30o的斜坡正对着“主山峰”前行700米,到达B处,再测得“峰顶”C的仰角为60o , 如图,根据以上条件求出“主山峰”的高度?(测角仪的高度忽略不计,结果精确到1米.参考数据:(![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴.上有两个长方形![]() 和
和![]() ,这两个长方形的宽都是
,这两个长方形的宽都是![]() 个单位长度,长方形
个单位长度,长方形![]() 的长
的长![]() 是
是![]() 个单位长度,长方形
个单位长度,长方形![]() 的长
的长![]() 是
是![]() 个单位长度,点
个单位长度,点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且
,且![]() 两点之间的距离为
两点之间的距离为![]() .
.
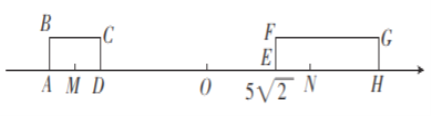
![]() 点
点![]() 在数轴上表示的数是 ,点
在数轴上表示的数是 ,点![]() 在数轴上表示的数是
在数轴上表示的数是
![]() 若线段
若线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 上有一点
上有一点![]() 以每秒
以每秒![]() 个单位长度的速度向右匀速运动,
个单位长度的速度向右匀速运动,![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,设运动的时间为
个单位长度的速度向左运动,设运动的时间为![]() 秒,问当
秒,问当![]() 为多少时,原点
为多少时,原点![]() 恰为线段
恰为线段![]() 的三等分点?
的三等分点?
![]() 若线段
若线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 上有一点
上有一点![]() ,长方形
,长方形![]() 以每秒
以每秒![]() 个单位长度的速度向右匀速运动,长方形
个单位长度的速度向右匀速运动,长方形![]() 保持不动,设运动时间为
保持不动,设运动时间为![]() 秒,是否存在一个
秒,是否存在一个![]() 的值,使以
的值,使以![]() 三点为顶点的三角形是直角三角形?若存在,求
三点为顶点的三角形是直角三角形?若存在,求![]() 的值;不存在,请说明理由.
的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
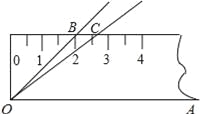
【题目】如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为 cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com