
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】解:(1)设抛物线顶点为E,根据题意OA=4,OC=3,得:E(2,3)。
设抛物线解析式为![]() ,
,
将A(4,0)坐标代入得:0=4a+3,即![]() 。
。
∴抛物线解析式为![]() 即
即![]() 。
。
(2)设直线AC解析式为![]() (k≠0),
(k≠0),
将A(4,0)与C(0,3)代入得:![]() ,解得:
,解得: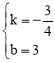 。
。
∴直线AC解析式为![]() 。
。
与抛物线解析式联立得: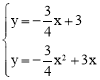 ,解得:
,解得:![]() 或
或![]() 。
。
∴点D坐标为(1,![]() )。
)。
(3)存在,分两种情况考虑:
①当点M在x轴上方时,如图1所示:
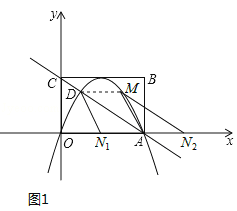
四边形ADMN为平行四边形,DM∥AN,DM=AN,
由对称性得到M(3,![]() ),即DM=2,故AN=2,
),即DM=2,故AN=2,
∴N1(2,0),N2(6,0)。
②当点M在x轴下方时,如图2所示:
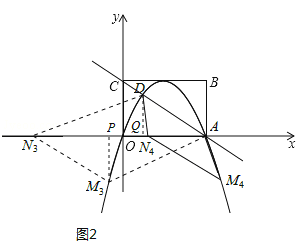
过点D作DQ⊥x轴于点Q,过点M作MP⊥x轴于点P,可得△ADQ≌△NMP,
∴MP=DQ=![]() ,NP=AQ=3。
,NP=AQ=3。
将yM=![]() 代入抛物线解析式得:
代入抛物线解析式得:
![]() ,
,
解得:xM=![]() 或xM=
或xM=![]() 。
。
∴xN=xM-3=![]() 或
或![]() ,
,
∴N3(![]() ,0),N4(
,0),N4(![]() ,0)。
,0)。
综上所述,满足条件的点N有四个:
N1(2,0),N2(6,0),N3(![]() ,0),N4(
,0),N4(![]() ,0)。
,0)。
【解析】
试题(1)由OA的长度确定出A的坐标,再利用对称性得到顶点坐标,设出抛物线的顶点形式![]() ,将A的坐标代入求出a的值,即可确定出抛物线解析式;。
,将A的坐标代入求出a的值,即可确定出抛物线解析式;。
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,确定出直线AC解析式,与抛物线解析式联立即可求出D的坐标。
(3)存在,分两种情况考虑:如图所示,当四边形ADMN为平行四边形时,DM∥AN,DM=AN,由对称性得到M(3,![]() ),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得△ADQ≌△NMP,MP=DQ=
),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得△ADQ≌△NMP,MP=DQ=![]() ,NP=AQ=3,将y=
,NP=AQ=3,将y=![]() 代入得:
代入得:![]() ,求出x的值,确定出OP的长,由OP+PN求出ON的长即可确定出N坐标。
,求出x的值,确定出OP的长,由OP+PN求出ON的长即可确定出N坐标。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A. B为数轴上两点,AB=15,且OA:OB=2.
(1)A、B对应的数分别为___、___;
(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A. B相距1个单位长度?
(3)点A. B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OBmOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(m-4,m+1)在x轴上,将点A右移8个单位,上移4个单位得到点B.

(1)则m= ;B点坐标( );
(2)连接AB交y轴于点C,则![]() = ;
= ;
(3)点D是x轴上一点,△ABD的面积为12,求D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,把点A(m,4)(m是实数)向右移动7个单位向下移动2个单位得到点B,点B向左移动3个单位向上移动6个单位得到点C,请解答:
(1) 点B,C的坐标是:B ,C ;
(2) 求△ABC的面积;
(3)若连接OC交线段AB于点D,且△ACD与△BCD的面积比不超过0.75时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(m-4,m+1)在x轴上,将点A右移8个单位,上移4个单位得到点B.

(1)则m= ;B点坐标( );
(2)连接AB交y轴于点C,则![]() = ;
= ;
(3)点D是x轴上一点,△ABD的面积为12,求D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
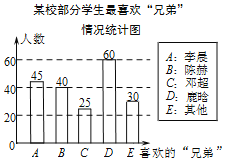
【题目】电视节目“奔跑吧兄弟”播出后深受中学生喜爱,小睿想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取部分学生进行抽查![]() 每人只能选一个自己最喜欢的“兄弟”
每人只能选一个自己最喜欢的“兄弟”![]() ,得到如图所示的统计图,
,得到如图所示的统计图,
请结合图中提供的信息解答下列问题:
![]() 若小睿所在学校有1800名学生,估计全校喜欢“鹿晗”兄弟的学生人数.
若小睿所在学校有1800名学生,估计全校喜欢“鹿晗”兄弟的学生人数.
![]() 小睿和小轩都喜欢“陈赫”,小彤喜欢“鹿晗”,从他们三人中随机抽选两人参加“撕名牌”游戏,求选中的两人中“一人喜欢陈赫,一人喜欢鹿晗”的概率
小睿和小轩都喜欢“陈赫”,小彤喜欢“鹿晗”,从他们三人中随机抽选两人参加“撕名牌”游戏,求选中的两人中“一人喜欢陈赫,一人喜欢鹿晗”的概率![]() 要求列表或画树状图
要求列表或画树状图![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):492,496,494,495,498,497,501,502,504,496,497,503,506,508,507,492,496,500,501,499,根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com