
【题目】如图,点O为原点,A. B为数轴上两点,AB=15,且OA:OB=2.
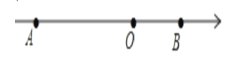
(1)A、B对应的数分别为___、___;
(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A. B相距1个单位长度?
(3)点A. B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OBmOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由。
【答案】(1)A、B对应的数分别为10、5;(2)2或![]() 秒;(3)当m=3时,4AP+3OBmOP为定值55.
秒;(3)当m=3时,4AP+3OBmOP为定值55.
【解析】
(1)根据题意求出OA、OB的长,根据数轴的性质解答;
(2)分点A在点B的左侧、点A在点B的右侧两种情况,列方程解答;
(3)根据题意列出关系式,根据定值的确定方法求出m即可.
(1)设OA=2x,则OB=x,
由题意得,2x+x=15,
解得,x=5,
则OA=10、OB=5,
∴A、B对应的数分别为10、5,
故答案为:10;5;
(2)设x秒后A. B相距1个单位长度,
当点A在点B的左侧时,4x+3x=151,
解得,x=2,
当点A在点B的右侧时,4x+3x=15+1,
解得,x=![]() ,
,
答:2或![]() 秒后A. B相距1个单位长度;
秒后A. B相距1个单位长度;
(3)设t秒后4AP+3OBmOP为定值,
由题意得,4AP+3OBmOP=4×[7t(4t10)]+3(5+3t)7mt
=(217m)t+55,
∴当m=3时,4AP+3OBmOP为定值55.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中![]() 表示小强从家出发后的时间,
表示小强从家出发后的时间,![]() 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量![]() 与
与![]() 之间关系的大致图象是( )
之间关系的大致图象是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 和
和![]() 的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数
的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数![]() 和
和![]() 互为中心对称函数.
互为中心对称函数.
![]() 求函数
求函数![]() 的中心对称函数;
的中心对称函数;
![]() 如图,在平面直角坐标系xOy中,E,F两点的坐标分别为
如图,在平面直角坐标系xOy中,E,F两点的坐标分别为![]() ,
,![]() ,二次函数
,二次函数![]() 的图象经过点E和原点O,顶点为
的图象经过点E和原点O,顶点为![]() 已知函数
已知函数![]() 和
和![]() 互为中心对称函数;
互为中心对称函数;
![]() 请在图中作出二次函数
请在图中作出二次函数![]() 的顶点
的顶点![]() 作图工具不限
作图工具不限![]() ,并画出函数
,并画出函数![]() 的大致图象;
的大致图象;
![]() 当四边形EPFQ是矩形时,请求出a的值;
当四边形EPFQ是矩形时,请求出a的值;
![]() 已知二次函数
已知二次函数![]() 和
和![]() 互为中心对称函数,且
互为中心对称函数,且![]() 的图象经过
的图象经过![]() 的顶点当
的顶点当![]() 时,求代数式
时,求代数式![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.

根据以上信息解答下列问题:
![]() 这次接受调查的市民总人数是______;
这次接受调查的市民总人数是______;
![]() 请补全条形统计图
请补全条形统计图![]() 如图
如图![]() ;
;
![]() 扇形统计图
扇形统计图![]() 如图
如图![]() 中,“电视”所对应扇形的圆心角为______度;
中,“电视”所对应扇形的圆心角为______度;
![]() 若该市约有80万人,请你估计将“手机上网”作为“获取新闻的最主要途径”的总人数.
若该市约有80万人,请你估计将“手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点D为BC边上的一点.
(1)以点C为旋转中心,将△ACD逆时针旋转90°,得到△BCE,请你画出旋转后的图形;
(2)延长AD交BE于点F,求证:AF⊥BE;
(3)若AC=![]() ,BF=1,连接CF,则CF的长度为______.
,BF=1,连接CF,则CF的长度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com