
分析 (1)原式利用多项式乘以多项式法则计算,合并后根据乘开的结果不含x3和x2项,求出m与n的值即可;
(2)原式利用多项式乘以多项式法则计算,把m与n的值代入计算即可求出值.
解答 解:(1)原式=x4-2x3-mx2+nx3-2nx2-mnx+3x2-6x-3m=x4+(n-2)x3+(3-m-2n)x2+(mn+6)x-3m,
由乘开的结果不含x3和x2项,得到n-2=0,3-m-2n=0,
解得:m=-1,n=2;
(2)当m=-1,n=2时,原式=m3+m2n+mn2-m2n-mn2-n3=m3-n3=-1-8=-9.
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
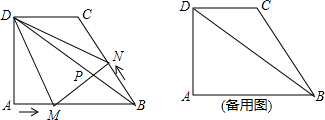
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
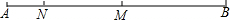 如图,已知点M是线段AB上的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=1.5cm,则线段AB=( )
如图,已知点M是线段AB上的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=1.5cm,则线段AB=( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么:
将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
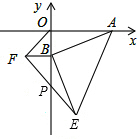 如图,点A的坐标为(8,0),点B是y轴负半轴上的任意一点,分别以OB,AB为直角边的第三第四象限作等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,则BP的长度为4.
如图,点A的坐标为(8,0),点B是y轴负半轴上的任意一点,分别以OB,AB为直角边的第三第四象限作等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,则BP的长度为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com