
 将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么:
将自然数按如下的顺序排列.在这样的排列下,9排在第3行第2列,那么:分析 (1)第1行第1列的数是1,第2行第1列的数是1+2=3,第3行第1列的数是1+2+3=6,…第n行第1列的数是1+2+3+4…+n=$\frac{1}{2}$n(n+1),由此算得答案即可;
(2)先将原图形变形成下图:观察新旧图形发现,新图形中每行从右往左数,第i个数位于原图形的第i行.新图形中每行从左往右数,第j个数位于原图形的第j列,且第n行左数第1个是(1+n)×n÷2.由此先找出2009在新图形中的位置,然后再变成它在原图中的位置.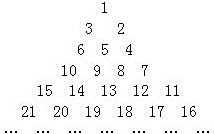
解答 解:(1)第1行第1列的数是1,
第2行第1列的数是1+2=3,
第3行第1列的数是1+2+3=6,
…
第n行第1列的数是1+2+3+4…+n=$\frac{1}{2}$n(n+1),
第2009行第1列的数是$\frac{1}{2}$×2009×2010=2019045;
(2)先找出2009所在的行数.
因为$\frac{1}{2}$×62×63=1953,$\frac{1}{2}$×63×64=2016,所2009在新图的第64行.
第64行左数第一个数是1954,
1953+56=2009.
根据2009-1953=56和64-56+1=9,可知2009在第56行第9列.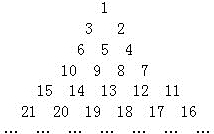
点评 此题考查数字的变化规律,找出数字的运算规律,利用规律解决问题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
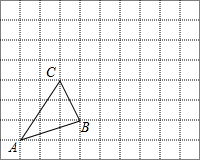 如图,每个小正方形边长为1cm,
如图,每个小正方形边长为1cm,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
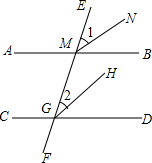 如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,求证:MN∥GH.
如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,求证:MN∥GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com