
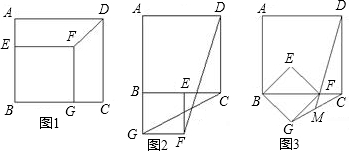
分析 (1)如图,连接BF,根据正方形的性质可以得到∠FBC=∠CBD=45°,由此推出∠FBD=∠GBC=90°,BF=$\sqrt{2}$BG,BD=$\sqrt{2}$BC,由此即可证△BFD、△BGC相似,然后利用相似三角形的性质即可得到结论;
(2)由于将图1中的正方形BEFG绕B点顺时针旋转90°,DF的延长线交CG于M,那么B、E、D三点在同一条直线上,根据正方形的性质可以得到∠FBD=∠GBC=90°,BF=$\sqrt{2}$BG,BD=$\sqrt{2}$BC,由此即可证△BFD、△BGC相似,然后利用相似三角形的性质即可得到结论;
(3)将图1中的正方形BEFG绕B点逆时针旋转β(0°<β<90°),如图所示,和(1)(2)一样证明△BFD、△BGC相似即可解决问题.
解答 解:(1)如图2,连接BF,
∵四边形ABCD、四边形BEFG是正方形,
∴∠FBC=∠CBD=45°,
∴∠FBD=∠GBC=90°,
∵BF=$\sqrt{2}$BG,BD=$\sqrt{2}$BC,
∴△BFD∽△BGC,
∴∠BCG=∠BDF,$\frac{FD}{CG}=\frac{BF}{BG}$
∵∠DMC=180°-∠BCG-∠BCD-∠CDF
=180°-∠BDF-∠BCD-∠CDF
=180°-(∠BDF+∠CDF)-∠BCD
=180-45°-90°
=45°,
∴$\frac{DF}{CG}=\sqrt{2}$,∠DMC=45°;
故答案为$\sqrt{2}$,45°.
(2)如图2,
∵将图1中的正方形BEFG绕B点顺时针旋转90°,
∴B、E、D三点在同一条直线上
∵四边形ABCD、四边形BEFG是正方形,
∴∠FBC=∠CBD=45°,
∴∠FBD=∠GBC=90°,
∵BF=$\sqrt{2}$BG,BD=$\sqrt{2}$BC,
∴△BFD∽△BGC,
∴∠BCG=∠BDF,$\frac{FD}{CG}=\frac{BF}{BG}$
∵∠DMC=180°-∠BCG-∠BCD-∠CDF
=180°-∠BDF-∠BCD-∠CDF
=180°-(∠BDF+∠CDF)-∠BCD
=180-45°-90°
=45°,
∴$\frac{DF}{CG}=\sqrt{2}$,∠DMC=45°;
(3)如图4,
如图4
∵四边形ABCD、四边形BEFG是正方形,
∴∠FBD=∠GBC,BF=$\sqrt{2}$BG,BD=$\sqrt{2}$BC,
∴△BFD∽△BGC,
∴$\frac{DF}{CG}=\sqrt{2}$,∠BCM=∠BDM,
∵∠DMC=180°-∠DCM-∠CDF
=180°-(∠BCD-∠BCM)-∠CDF
=180°-∠BCD+∠BCM-(∠CDB+∠BDM)
=180°-∠BCD-∠BDM-∠CDB-∠BDM
=180°-∠BCD-∠CDB
=180-90°-45°
=45°,
∴∠DMC=45°;
∴$\frac{DF}{CG}=\sqrt{2}$,∠DMC=45°
点评 此题是四边形综合题,主要考查了旋转及正方形的性质,综合性比较强,通过利用正方形的性质构造相似三角形的相似条件,然后利用相似三角形性质就可以解决问题,判断△BFD∽△BGC是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
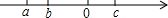 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )| A. | a-2b | B. | 2b+c | C. | -2a+c | D. | a-2b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°
如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
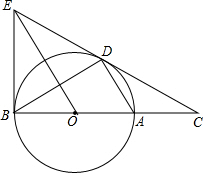 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
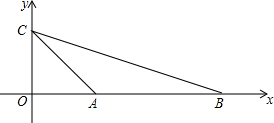 如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).
如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com