
 如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°
如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°分析 (1)由“直线y=x+3分别交x,y轴于点D,C”可得出C、D点的坐标,根据∠ODC的正切值即可求出∠ODC的度数,再由直线m∥直线CD,根据“两直线平行,同旁内角互补”即可得出∠PBO的值;
(2)断定PB•CQ是定值.依据角的计算,可得出“∠COQ=∠BPO,∠CQO=∠BOP”,由此得出△COQ∽△BPO,根据相似三角形的性质即可得出$\frac{CQ}{BO}=\frac{CO}{BP}$,再结合B、C点的坐标即可得出结论;
(3)过点Q作QE⊥m于点E,由B、C点的坐标可知“∠OBC=45°,BC=3$\sqrt{2}$”,结合(1)的结论可得出∠PBC=90°,结合QE⊥m、直线m∥直线CD可得出QE=CB=3$\sqrt{2}$,在Rt△QEP中由勾股定理可得出PQ2=QE2+PE2,将PE换成PB-CQ,再代入PB•CQ=9即可得出结论.
解答 解:(1)令x=0,则y=3,
即点C的坐标为(0,3);
令y=0,则有x+3=0,
解得:x=-3,即点D的坐标为(-3,0).
又∵OB=OC,
∴OC=OD=OB=3.
∵tan∠ODC=$\frac{OC}{OD}$=1,
∴∠ODC=45°,
∵直线m∥直线CD,
∴∠ODC+∠PBO=180°,
∴∠PBO=135°.
故答案为:135
(2)PB•CQ是定值,理由如下:
∠OCQ=∠ODC+∠COD=45°+90°=135°=∠PBO,
∵∠COQ+∠CQO=180°-∠OCQ=45°,∠BOP+∠BPO=180°-∠PBO=45°,
∴∠COQ+∠CQO=∠BOP+∠BPO=45°,
又∵∠COQ+∠BOP=∠BOC-∠POQ=90°-45°=45°,
∴∠COQ=∠BPO,∠CQO=∠BOP,
∴△COQ∽△BPO,
∴$\frac{CQ}{BO}=\frac{CO}{BP}$,即PB•CQ=OB•OC=9.
(3)证明:过点Q作QE⊥m于点E,如图1所示.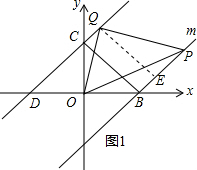
∵OB=OC=3,∠BOC=90°,
∴∠OBC=45°,BC=3$\sqrt{2}$.
∴∠PBC=∠PBO-∠OBC=135°-45°=90°,
又∵QE⊥m,
∴CB∥QE,∠PEQ=90°.
∵直线m∥直线CD,
∴四边形BEQC为矩形,
∴QE=CB=3$\sqrt{2}$.
在Rt△QEP中,∠PEQ=90°,PE=PB-CQ,QE=3$\sqrt{2}$,
∴PQ2=QE2+PE2=18+(PB-CQ)2,
又∵PB•CQ=9,
∴PQ2=2PB•CQ+(PB-CQ)2=PB2+CQ2.
点评 本题考查了平行线的性质、角的计算、角的正切值、相似三角形的判定及性质和勾股定理,解题的关键是:(1)找出∠ODC=45°;(2)证出△COQ∽△BPO;(3)根据勾股定理得出PQ2=QE2+PE2.本题属于中档题,难度不大,解决该题型题目时,根据角的计算找出相等的角,根据相似三角形的判定定理找出相似三角形,再根据相似三角形的性质得出边与边之间的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
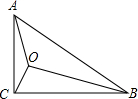 如图,在Rt△ABC中,∠C=90°,AC=2cm,BC=2$\sqrt{3}$cm,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°.按要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′).
如图,在Rt△ABC中,∠C=90°,AC=2cm,BC=2$\sqrt{3}$cm,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°.按要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
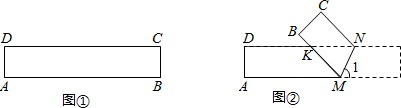
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ?ABCD是中心对称图形 | B. | △AOB与△BOC的面积相等 | ||
| C. | △AOB≌△COD | D. | △AOB≌△BOC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
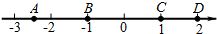 如图,数轴上有A、B、C、D四点,其中表示互为相反数的两个实数所对应的点是( )
如图,数轴上有A、B、C、D四点,其中表示互为相反数的两个实数所对应的点是( )| A. | 点A与点D | B. | 点A与点C | C. | 点B与点D | D. | 点B与点C |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.25×10-7m | B. | 2.5×106m | C. | 2.5×10-6m | D. | 2.5×10-8m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
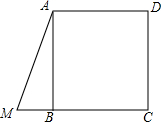 如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.
如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com