
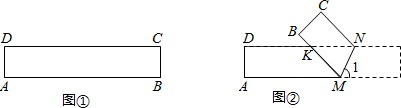
���� ��1�����ݾ��ε����ʺ��۵������������KNM����KMN�Ķ����������������ڽǺͼ�����⣻
��2����M����ME��DN������ΪE��ͨ��֤��NK��1���������������ʽ�ɵá�MNK�����������С�ڣ�
��3�������һ��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ�
�������������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC�������������⣮
��� �⣺��1�����ı���ABCD�Ǿ��Σ�
��AM��DN��
���KNM=��1��
�ߡ�1=70�㣬
���KNM=��KMN=��1=70�㣬
���MKN=40�㣮
��2�����ܣ���ͼ1��
��M����ME��DN������ΪE����ME=AD=1��
�ߡ�KNM=��KMN��
��MK=NK��
�֡�MK��ME��
��NK��1��
���MNK�����=$\frac{1}{2}$ NK•ME��$\frac{1}{2}$��
���MNK�������������$\frac{1}{2}$��
��3�������������
���һ��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ�
MK=MB=x����AM=5-x��
�ɹ��ɶ�����1 2+��5-x�� 2=x 2��
���x=2.6��
��MD=ND=2.6��
S��MNK=S��MNK=$\frac{1��2.6}{2}$=1.3��
�������������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC��
MK=AK=CK=x����DK=5-x��
ͬ���ɵã�MK=NK=2.6��
��MD=1��
��S��MNK=$\frac{1��2.6}{2}$=1.3��
��MNK��������ֵΪ1.3��
���� �������ı����ۺ��⣬��Ҫ������ε����ʡ���ԳƱ任�Լ����ɶ��������ã�����ͼ���ǽⱾ��Ĺؼ���


 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
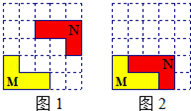 ��5��5����ֽ�н�ͼ���е�ͼ��Nƽ�ƺ��λ����ͼ����ʾ����ô����ƽ������ȷ���ǣ�������
��5��5����ֽ�н�ͼ���е�ͼ��Nƽ�ƺ��λ����ͼ����ʾ����ô����ƽ������ȷ���ǣ�������| A�� | �������ƶ�1���������ƶ�1�� | B�� | �������ƶ�1���������ƶ�2�� | ||
| C�� | �������ƶ�2���������ƶ�1�� | D�� | �������ƶ�2���������ƶ�2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
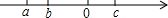 ʵ��a��b��c�������ϵ�λ����ͼ��ʾ����$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{��a-c��}^{2}}$-$\sqrt{{��b+c��}^{2}}$�Ľ��Ϊ��������
ʵ��a��b��c�������ϵ�λ����ͼ��ʾ����$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{��a-c��}^{2}}$-$\sqrt{{��b+c��}^{2}}$�Ľ��Ϊ��������| A�� | a-2b | B�� | 2b+c | C�� | -2a+c | D�� | a-2b+c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����?ABCD�У�AD=5��AB=3��AEƽ�֡�BAD��BC���ڵ�E�����߶�BE��EC�ij��ȷֱ�Ϊ��������
��ͼ����?ABCD�У�AD=5��AB=3��AEƽ�֡�BAD��BC���ڵ�E�����߶�BE��EC�ij��ȷֱ�Ϊ��������| A�� | 1��4 | B�� | 4��1 | C�� | 2��3 | D�� | 3��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=x+3�ֱ�x��y���ڵ�D��C����B��x���ϣ�OB=OC������B��ֱ��m��CD����P��Q�ֱ�Ϊֱ��m��ֱ��CD�ϵĶ��㣬�ҵ�P��x����Ϸ��������POQ=45��
��ͼ��ֱ��y=x+3�ֱ�x��y���ڵ�D��C����B��x���ϣ�OB=OC������B��ֱ��m��CD����P��Q�ֱ�Ϊֱ��m��ֱ��CD�ϵĶ��㣬�ҵ�P��x����Ϸ��������POQ=45���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com