
【题目】如图,已知二次函数y=ax2+bx+c(a#0)的图象如图所示,给出以下四个结论:
①abc=0,②a+b+c>0,③b=3a, ④4ac—b2<0;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解 :∵二次函数y=ax2+bx+c图象经过原点,
∴c=0,
∴abc=0,故①正确;
∵x=1时,y<0,
∴a+b+c<0,故②不正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴是x=![]() ,
,
∴![]() =
=![]() ,
,
∴b=3a,故③正确;
∵二次函数y=ax2+bx+c图象与x轴有两个交点,
∴△>0,
∴b24ac>0,4acb2<0,故④正确;
综上,可得正确结论有3个:①③④。
故答案为 :C .
首先根据二次函数y=ax2+bx+c的图象经过原点,可得c=0,所以abc=0;然后根据x=1时,y<0,可得a+b+c<0;根据抛物线的对称轴知b=3a;最后根据二次函数y=ax2+bx+c图象与x轴有两个交点,可得△>0,所以b2-4ac>0,4ac-b2<0,据此解答即可 。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:

(1)用一种正多边形镶嵌平面
例如,用 6 个全等的正三角形镶嵌平面,摆放方案如图所示:
若用 m 个全等的正 n 边形镶嵌平面,求出 m,n 应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有 n 个,设这 n 个正多边形的边数分别为 x1,x2,…,xn,求出 x1,x2,…,xn 应满足的关系式.(用含 n 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.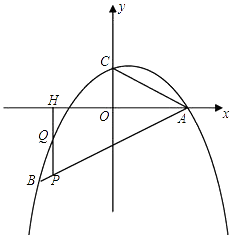
(1)试求此二次函数的解析式;
(2)试证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=-x+4的图象如图所示.
(1)在同一坐标系中,作出一次函数y=2x-5的图象;
(2)用作图象的方法解方程组![]()
(3)求一次函数y=-x+4与y=2x-5的图象与x轴所围成的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角.
(1)如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.
(2)如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.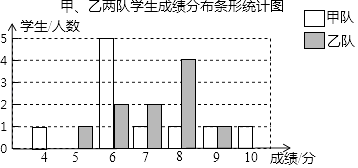
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a= , b=c= .
平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
甲队 | a | 6 | c | 2.76 | 90% | 20% |
乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(2)小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com