
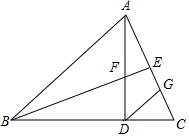
 如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.分析 (1)只要证明△BDF≌△ADC,推出BD=AD,推出∠BAD=∠ABD=2∠CBE=2∠DAC即可解决问题.
(2)延长BE、DG交于点K.想办法证明Rt△AEF≌Rt△KEG即可.
解答 证明:(1)∵AD⊥BC,
∴∠ADC=90°
∵AB=BC,E为AC中点,
∴∠ABE=∠CBE=$\frac{1}{2}$∠ABC,BE⊥AC,
∴∠BEC=90°,
∴180°-∠C-∠ADC=180°-∠C-∠BEC
即∠CBE=∠CAD,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠FDB=∠CDA=90°}\\{∠FBD=∠CAD}\\{BF=AC}\end{array}\right.$,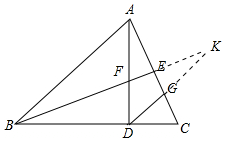
∴△BDF≌△ADC,
∴BD=AD,
∴∠BAD=∠ABD=2∠CBE=2∠DAC.
(2)延长BE、DG交于点K.
∵DG∥AB,
∴∠CGD=∠CAB,∠K=∠ABE,
∵∠BAC=∠C,
∴∠CGD=∠C
∵∠K=∠CBE=∠CAD
∠AEF=∠KEG=90,°∠EAF=∠EKG,
∴DG=DC,DK=BD,
∴DG=DF,DK=BD=AD,
∴DK-DG=AD-DF,即GK=AF
在Rt△AEF和Rt△KEG中
$\left\{\begin{array}{l}{∠AEF=∠KEG=90°}\\{∠EAF=∠K}\\{AF=GK}\end{array}\right.$,
∴Rt△AEF≌Rt△KEG (AAS),
∴EF=EG.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:选择题
 某校团委准备举办学生绘画展览,为美化画面,在长8dm、宽为5dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22dm2(如图),若设彩纸的宽度为x分米,则可得方程为( )
某校团委准备举办学生绘画展览,为美化画面,在长8dm、宽为5dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22dm2(如图),若设彩纸的宽度为x分米,则可得方程为( )| A. | 40-10x-16x=18 | B. | (8-x)(5-x)=18 | C. | (8-2x)(5-2x)=18 | D. | 40-5x-8x+4x2=22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com