
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,又已知位于
,又已知位于![]() 轴右侧且垂直于
轴右侧且垂直于![]() 轴的动直线
轴的动直线![]() ,沿
,沿![]() 轴正方向从
轴正方向从![]() 运动到
运动到![]() (不含
(不含![]() 点和
点和![]() 点),且分别交抛物线,线段
点),且分别交抛物线,线段![]() 以及
以及![]() 轴于点
轴于点![]() .
.
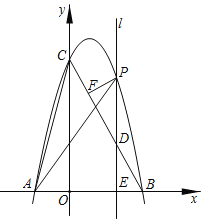
(1)求抛物线的表达式;
(2)连接![]() ,
,![]() ,当直线
,当直线![]() 运动时,求使得
运动时,求使得![]() 和
和![]() 相似的点
相似的点![]() 的坐标;
的坐标;
(3)作![]() ,垂足为
,垂足为![]() ,当直线
,当直线![]() 运动时,求
运动时,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() ;(3)
;(3)![]() .
.
【解析】
(1)将点A、B、C的坐标代入二次函数表达式,即可求解;
(2)只有当∠PEA=∠AOC时,PEA△∽AOC,可得:PE=4AE,设点P坐标(4k-2,k),即可求解;
(3)利用Rt△PFD∽Rt△BOC得: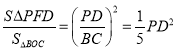 ,再求出PD的最大值,即可求解.
,再求出PD的最大值,即可求解.
(1)由已知,将![]() 代入
代入![]() ,∴
,∴![]() .
.
将点![]() 和
和![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() .∴抛物线的表达式为
.∴抛物线的表达式为![]() .
.
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 轴,
轴,
∴![]() ,
,
∵![]() ,
,
∴只有当![]() 时,
时,![]() ,
,
此时![]() ,即
,即![]() ,
,
∴![]() .
.
设点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() ,将
,将![]() 代入
代入![]() ,得
,得
![]() ,
,
解得![]() (舍去),
(舍去),![]() .
.
当![]() 时,
时,![]() .
.
∴![]() 点的坐标为
点的坐标为![]() .
.
(3)在![]() 中,
中,![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
由![]() ,知
,知![]() ,又
,又![]() ,
,
∴![]() ,
,
又![]() .
.
∴![]() .
.
∴当![]() 最大时,
最大时,![]() 最大.
最大.
由![]() ,
,![]() 可解得
可解得![]() 所在直线的表达式为
所在直线的表达式为![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() .
.
∴当![]() 时,
时,![]() 有最大值4.
有最大值4.
∴当![]() 时,
时,![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了创建全国文明城市知识竞赛活动,初一年级全体同学参加了竞赛.收集数据:现随机抽取初一年级30名同学“创文知识竞赛”成绩,分数如下(单位:分):
90 | 85 | 68 | 92 | 81 | 84 | 95 | 93 | 87 | 89 | 78 | 99 | 89 | 85 | 97 |
88 | 81 | 95 | 86 | 98 | 95 | 93 | 89 | 86 | 84 | 87 | 79 | 85 | 89 | 82 |
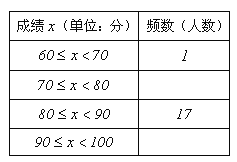

⑴请将图表中空缺的部分补充完整;
⑵学校决定表彰“创文知识竞赛”成绩在90分以上的同学,根据上表统计结果估计该校初一年级360人中,约有多少人将获得表彰;
⑶“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
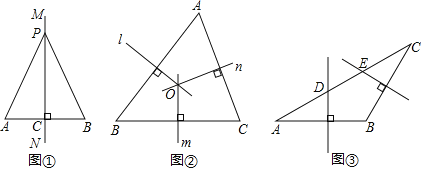
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
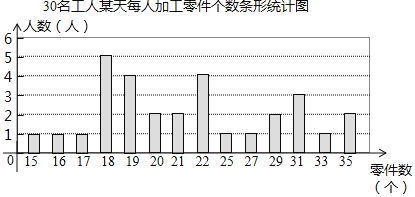
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )

A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】群芳雅苑花卉基地出售两种花卉,其中马蹄莲每株4.5元,康乃馨每株6元.如果同一客户所购的马蹄莲数量多于1000株,那么所有的马蹄莲每株还可优惠0.3元.现某鲜花店向群芳雅苑花卉基地采购马蹄莲800~1200株、康乃馨若干株本次采购共用了9000元.然后再以马蹄莲每株5.5元、康乃馨每株8元的价格卖出.(注:800~1200株表示采购株数大于或等于800株,且小于或等于1200株;利润=销售所得金额﹣进货所需金额)
(1)设鲜花店销售完这两种鲜花获得的利润为y元,采购马蹄莲x株,求y与x之间的函数关系式;
(2)若该鲜花店购进的马蹄莲多于1000株,采购马蹄莲多少时才能使获得的利润不少于2890元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com