
����Ŀ��Ⱥ����Է���ܻ��س������ֻ��ܣ�����������ÿ��4.5Ԫ������ܰÿ��6Ԫ�����ͬһ�ͻ���������������������1000�꣬��ô���е�������ÿ�껹���Ż�0.3Ԫ����ij�ʻ�����Ⱥ����Է���ܻ��زɹ�������800��1200�ꡢ����ܰ�����걾�βɹ�������9000Ԫ��Ȼ������������ÿ��5.5Ԫ������ܰÿ��8Ԫ�ļ۸���������ע��800��1200���ʾ�ɹ��������ڻ����800�꣬��С�ڻ����1200�ꣻ�����������ý����������
��1�����ʻ����������������ʻ���õ�����ΪyԪ���ɹ�������x�꣬��y��x֮��ĺ�����ϵʽ��
��2�������ʻ��깺��������������1000�꣬�ɹ�����������ʱ����ʹ��õ���������2890Ԫ��
���𰸡���1����800��x��1000ʱ��y��3000��0.5x����1000��x��1200ʱ��y��3000��0.1x����2���ɹ�����������1000���Ҳ�����1100��ʱ����ʹ��õ���������2890Ԫ��
��������
��1���������⣬���÷������۵ķ����������y��x�ĺ�����ϵʽ��
��2�����ݣ�1���еĺ�����ϵʽ����3000��0.1x��2890���������x��ȡֵ��Χ��������Խ����
�⣺��1����800��x��1000ʱ��
y����5.5��4.5��x+��8��6����![]() ��3000��0.5x��
��3000��0.5x��
��1000��x��1200ʱ��
y����5.5��4.5+0.3��x+![]() ��3000��0.1x��
��3000��0.1x��
��2����3000��0.1x��2890��
��ã�x��1100��
�𣺲ɹ�����������1000���Ҳ�����1100��ʱ����ʹ��õ���������2890Ԫ��


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ������֪λ��
������֪λ��![]() ���Ҳ��Ҵ�ֱ��
���Ҳ��Ҵ�ֱ��![]() ��Ķ�ֱ��
��Ķ�ֱ��![]() ����
����![]() ���������
���������![]() �˶���
�˶���![]() ������
������![]() ���
���![]() �㣩���ҷֱ������ߣ��߶�
�㣩���ҷֱ������ߣ��߶�![]() �Լ�
�Լ�![]() ���ڵ�
���ڵ�![]() ��
��
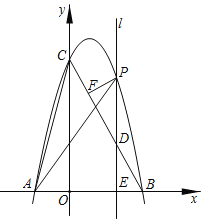
��1���������ߵı���ʽ��
��2������![]() ��
��![]() ����ֱ��
����ֱ��![]() �˶�ʱ����ʹ��
�˶�ʱ����ʹ��![]() ��
��![]() ���Ƶĵ�
���Ƶĵ�![]() �����ꣻ
�����ꣻ
��3����![]() ������Ϊ
������Ϊ![]() ����ֱ��
����ֱ��![]() �˶�ʱ����
�˶�ʱ����![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������Ϊ3����Ϊ8�ij�����������������ˮƽ�����ϣ�����ʢ��ˮ��ˮ���Ϊ6���Ƶ���һ�ⳤ������ת��б��ˮ��ǡ�ô��������ڱ�Ե��ͼ2�Ǵ�ʱ��ʾ��ͼ����ͼ2��ˮ��߶�Ϊ�� ��
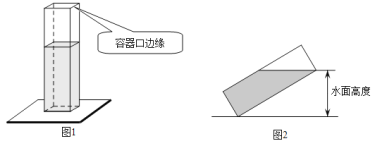
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������£�ij����ר������ij��Ʒ�Ƶ�������Ͳ���ɱ�Ϊ![]() Ԫ/����ÿ������
Ԫ/����ÿ������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.
��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.

��1����![]() ��
��![]() ֮��ĺ�����ϵ��
֮��ĺ�����ϵ��
��2������涨ÿ��������Ͳ��������������![]() ���������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
���������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
��3��������������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������![]() Ԫ����ȷ����������Ͳ���۵��۵ķ�Χ.
Ԫ����ȷ����������Ͳ���۵��۵ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����ADE��Ϊ�ȱ������Σ���OAC���е㣬��D��A����BO�ϣ�����OE��EC����AB��4����OE����СֵΪ_____��
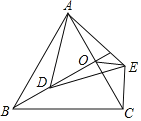
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ���ڡ�����Σ�շ����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ�˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������ˣ�
��1������ѡȡ�����ķ����������һ���� ����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����γ������˷��֣����ܵ��˵ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��
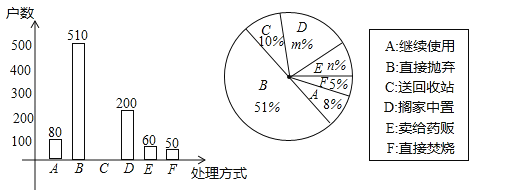
��m= ��n= ��
����ȫ����ͳ��ͼ��
�����ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��
����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ����֪��![]() �У�
�У�![]() ,
,![]() ,�ӳ�
,�ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ����
����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶����
��Ϊ�뾶����![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ,����
,����![]() ��
��
��������֤��![]() �ǡ�
�ǡ�![]() �����ߣ�
�����ߣ�
��������AB=2,��ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
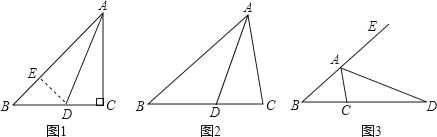
����Ŀ������ABC�У���ACB=2��B����ͼ��������C=90�㣬ADΪ��BAC�Ľ�ƽ����ʱ����AB�Ͻ�ȡAE=AC������DE����֤AB=AC+CD��
��1����ͼ��������C��90�㣬ADΪ��BAC�Ľ�ƽ����ʱ���߶�AB��AC��CD����������������ϵ������Ҫ֤������ֱ��д����IJ��룺
��2����ͼ������ADΪ��ABC�����ƽ����ʱ���߶�AB��AC��CD����������������ϵ����д����IJ��룬������IJ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
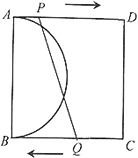
����Ŀ����ͼ����������ABCD�У�![]() ����ABΪֱ������ԲO����P�ӵ�A��������AD������ÿ��1����λ���ٶ����D�˶�����Q�ӵ�C��������C8������ÿ��3����λ���ٶ����B�˶�������ͬʱ��ʼ�˶�����һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ
����ABΪֱ������ԲO����P�ӵ�A��������AD������ÿ��1����λ���ٶ����D�˶�����Q�ӵ�C��������C8������ÿ��3����λ���ٶ����B�˶�������ͬʱ��ʼ�˶�����һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ![]() .
.
(1)���MΪ��Բ![]() ������һ�㣬��DM�����ֵΪ______����СֵΪ______.
������һ�㣬��DM�����ֵΪ______����СֵΪ______.
(2)��PQ����Բ![]() �ڵ�F�͵�G(��F�ڵ�G���Ϸ�)����
�ڵ�F�͵�G(��F�ڵ�G���Ϸ�)����![]() ʱ����
ʱ����![]() �ij��ȣ�
�ij��ȣ�
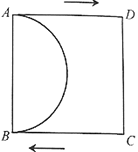
(3)���˶������У�PQ�Ͱ�Բ![]() �ܷ����У������У��������ʱl��ֵ�����������У���˵�����ɣ�
�ܷ����У������У��������ʱl��ֵ�����������У���˵�����ɣ�
(4)��N�ǰ�Բ![]() ��һ�㣬��
��һ�㣬��![]() �����˶�
�����˶�![]() ʱ��PQ���Բ
ʱ��PQ���Բ![]() �Ľ���ǡ��Ϊ��N��ֱ��д����ʱt��ֵ��
�Ľ���ǡ��Ϊ��N��ֱ��д����ʱt��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com