
����Ŀ��С������ѧϰС����̽����ת��ƽ�Ʊ任����ͼ��ABC��DEF��Ϊ����ֱ�������Σ�����������ֱ�ΪA��1��1����B��2��2����C��2��1����D�� ![]() ��0����E��2
��0����E��2 ![]() ��0����F��
��0����F�� ![]() ����
���� ![]() ����
����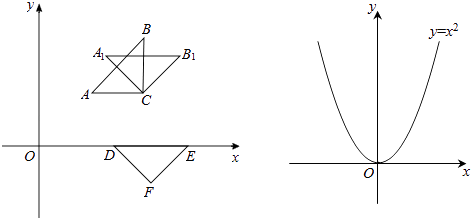
��1�����ǽ���ABC��C�㰴˳ʱ�뷽����ת45��õ���A1B1C1 �� ����д����A1 �� B1�����꣬���ж�A1C��DF��λ�ù�ϵ��
��2�����ǽ���ABC��ԭ�㰴˳ʱ�뷽����ת45�㣬������ת���������ǡ����������������������y=2 ![]() x2+bx+c�ϣ�����������������������߽���ʽ��
x2+bx+c�ϣ�����������������������߽���ʽ��
��3�����Ǽ���̽�������ֽ���ABC��ij������ת45�㣬����ת���������ǡ����������������������y=x2�ϣ���������ת�������ε�ֱ�Ƕ���P�����꣬����ֱ��д����P���������꣮
���𰸡�
��1��
�⣺A1��2�� ![]() ��1+
��1+ ![]() ����B1��2+
����B1��2+ ![]() ��1+
��1+ ![]() ����
����
A1C��DF��λ�ù�ϵ��ƽ��
��2��
�⣺�ߡ�ABC��ԭ�㰴˳ʱ�뷽����ת45���������μ�Ϊ��DEF��
��ٵ������߾�����D��Eʱ����������ɵã�
![]() ��
��
��� ![]()
��y= ![]() x2��12x+
x2��12x+ ![]() ��
��
�ڵ������߾�����D��Fʱ����������ɵã�
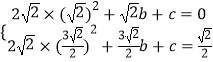 ��
��
��� ![]()
��y= ![]() x2��11x+
x2��11x+ ![]() ��
��
�۵������߾�����E��Fʱ����������ɵã�
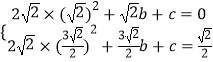 ��
��
��� ![]()
��y= ![]() x2��13x+
x2��13x+ ![]()
��3��
�⣺����ת�����У��������������Σ�
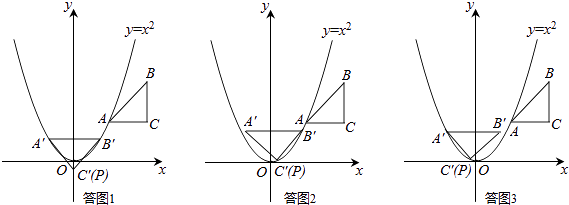
��˳ʱ����ת45�㣬��A��B�����������ϣ����ͼ1��ʾ��
����õ�P����Ϊ��0�� ![]() ����
����
��˳ʱ����ת45�㣬��B��C�����������ϣ����ͼ2��ʾ��
���B�䣬C��ĺ�����ֱ�Ϊx1��x2��
��֪��ʱB��C����һ��������ƽ����ƽ�У�����ֱ��B��C��Ľ���ʽΪy=x+b��
����y=x2��y=x+b�ã�x2=x+b����x2��x��b=0��
��x1+x2=1��x1x2=��b��
��B��C��=1������������ã�|x1��x2|= ![]() ��
��
�ࣨx1��x2��2= ![]() ������x1+x2��2��4x1x2=
������x1+x2��2��4x1x2= ![]()
��1+4b= ![]() �����b=-
�����b=- ![]() ��
��
��x2��x+ ![]() =0�����x=
=0�����x= ![]() ��x=
��x= ![]() ��
��
�ߵ�C��ĺ������С����x= ![]() ��
��
��x= ![]() ʱ��y=x2=
ʱ��y=x2= ![]() ��
��
��P�� ![]() ��
�� ![]() ����
����
��˳ʱ����ת45�㣬��C��A�����������ϣ����ͼ3��ʾ��
���C�䣬A��ĺ�����ֱ�Ϊx1��x2��
��֪��ʱC��A�������������ƽ����ƽ�У�����ֱ��C��A��Ľ���ʽΪy=��x+b��
����y=x2��y=��x+b�ã�x2=��x+b����x2+x��b=0��
��x1+x2=��1��x1x2=��b��
��C��A��=1������������ã�|x1��x2|= ![]() ��
��
�ࣨx1��x2��2= ![]() ������x1+x2��2��4x1x2=
������x1+x2��2��4x1x2= ![]()
��1+4b= ![]() �����b=-
�����b=- ![]() ��
��
��x2+x+ ![]() =0�����x=
=0�����x= ![]() ��x=
��x= ![]() ��
��
�ߵ�C��ĺ�����ϴ�x= ![]() ��
��
��x= ![]() ʱ��y=x2=
ʱ��y=x2= ![]() ��
��
��P�� ![]() ��
�� ![]() ����
����
����ʱ����ת45�㣬��A��B�����������ϣ�
��Ϊ��ʱ����ת45���ֱ��A��B����y��ƽ�У���ˣ������������ֻ����һ�����㣬�ʴ������β����ڣ�
����ʱ����ת45�㣬��B��C�����������ϣ����ͼ4��ʾ��
���ͬ��������ã�P�� ![]() ��
�� ![]() ����
����
����ʱ����ת45�㣬��C��A�����������ϣ����ͼ5��ʾ��
���ͬ��������ã�P�� ![]() ��
�� ![]() ����
����
������������P����������0�� ![]() ������
������ ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ��
��
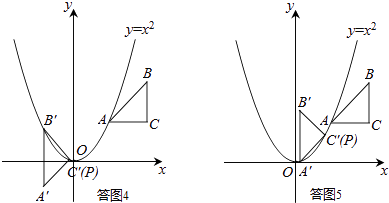
����������1������ת���ʼ�����ֱ�������α߽ǹ�ϵ��⣻��2��������ȷ��ABC��ԭ�㰴˳ʱ�뷽����ת45���������μ�Ϊ��DEF��Ȼ�����������������ۣ��ֱ������⣻��3����ת������˳ʱ�롢��ʱ�����ֿ��ܣ������������ϵĵ��е�A�͵�B����B�͵�C����C�͵�D���ֿ��ܣ���˹������ֿ��ܵ����Σ���Ҫ�������ۣ�����©�⣮
�����㾫����������Ҫ������ƽ�Ƶ����ʺ���ת�����ʵ����֪ʶ�㣬��Ҫ���բپ���ƽ��֮���ͼ����ԭ����ͼ�εĶ�Ӧ�߶�ƽ�У�����ͬһֱ���ϣ�����ȣ���Ӧ����ȣ�ͼ�ε���״���С��û�з����仯���ھ���ƽ�ƺ�Ӧ���������߶�ƽ�У�����ͬһֱ���ϣ�����ȣ�����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��˲�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������εĶ��壬���Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
��1����֪����ͼ1���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C����A=70�㣬��B=80�㣮���C����D�Ķ�����
��2����̽�����ȶԽ��ı��Ρ�����ʱ��
��С�컭��һ�����ȶԽ��ı��Ρ�ABCD����ͼ2�������С�ABC=��ADC��AB=AD����ʱ������CB=CD����������֤���˽��ۣ�
���ɴ�С����룺���������⡮�ȶԽ��ı��Ρ�����һ���ڱ����ʱ����һ���ڱ�Ҳ��ȡ�������Ϊ���IJ�����ȷ������ȷ����֤����������ȷ����ٳ�������
��3����֪���ڡ��ȶԽ��ı��Ρ�ABCD�У���DAB=60�㣬��ABC=90�㣬AB=5��AD=4����Խ���AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����y=kx���Ƿ����ʵ��k��ʹ�ô���ʽ��x2��y2����4x2��y2��+3x2��4x2��y2���ܻ���Ϊx4�����ܣ��������������������k��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�����꼶ѧ���������������������ȫ�����꼶ѧ���������ȡ�˲���ѧ��������һ���������Կ�Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A�������㣺B�������ã�C��������D�����������������Խ���������ͼ������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺ 
��1�����γ������Ե�ѧ������
��2����ͼ1�СϦ��Ķ������㣬��ͼ2����ͳ��ͼ����������
��3���������꼶��ѧ��3500�������ȫ���μ����������Ŀ���ԣ�����Ʋ����������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
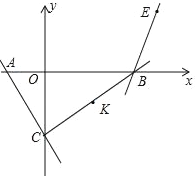
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��![]() x��
x��![]() ��x���ڵ�A����y���ڵ�C��ֱ��y=
��x���ڵ�A����y���ڵ�C��ֱ��y=![]() x��5
x��5![]() ��x���ڵ�B����ƽ������һ��E��������Ϊ��4��
��x���ڵ�B����ƽ������һ��E��������Ϊ��4��![]() ��������CB����K���߶�CB���е㣬��������M��N��������ֱ�Ϊ��a��0������a+1��0������K��������ƽ��
��������CB����K���߶�CB���е㣬��������M��N��������ֱ�Ϊ��a��0������a+1��0������K��������ƽ��![]() ����λ��������ƽ��
����λ��������ƽ��![]() ����λ��K�䣬����K�䣬E��M��N�ĵ�Ϊ������ı����ܳ����ʱ��a��ֵΪ_____��
����λ��K�䣬����K�䣬E��M��N�ĵ�Ϊ������ı����ܳ����ʱ��a��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ί�ٰ조�ҵ��й��Ρ�Ϊ�����֪ʶ�������ס�������ѧУ����������ȣ�������������ѧ���ɼ��ֱ�Ϊ70�֡�80�֡�90�֡�100�֣�������ͳ�����ݻ��������²�������ͳ��ͼ����

��У�ɼ�ͳ�Ʊ�
����/�� | ����/�� |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)��ͼ���У���80�֡��������ε�Բ�ĽǶ���Ϊ________��
(2)���㽫ͼ�ڲ���������
(3)����У�ɼ���ƽ���֣�
(4)������֪s��2��135��s��2��175������������������ݣ��Լס�����У�ɼ������������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�ֱ��y=��x+3��y=3x��5�ཻ��C�㣬�ֱ���x�ύ��A��B���㣮P��Q�ֱ�Ϊֱ��y=��x+3��y=3x��5�ϵĵ㣮
��1�����ABC�������
��2����P��Q����ԭ������ĶԳƣ���P������ꣻ
��3������QPC�ա�ABC����Q������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F�ֱ��ڱ�DC��AB�ϣ�DE=BF����ƽ���ı�����ֱ��EF�۵���ʹ�õ�B��C�ֱ�����B�䣬C�䴦���߶�EC�����߶�AF���ڵ�G������DG��B��G�� 
��֤��
��1����1=��2��
��2��DG=B��G��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���C������Ϊ��5��1���� �ٻ�����ABC����y��ԳƵġ�A1B1C1 �� ��д����C1�����ꣻ
������BC1 �� ������ƽ��ĸ����ȷ��һ����P��ʹ��B C1P����B C1Ϊ�ĵ���ֱ�������Σ�������B C1P����д������P������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com