
【题目】如图,已知⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连接EF.
(1)求证:CD是⊙A的切线;
(2)若⊙A的半径为2,tan∠BEF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
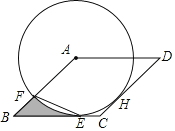
【答案】(1)详见解析;(2)![]()
【解析】
(1)作AH⊥CD于H,连结AE,AC, 根据菱形性质得到AC平分∠BCD,AE⊥BC,AH⊥CD,得到AE=AH,即CD为⊙A的半径,所以⊙A与边CD也相切;(2)tan∠BEF=![]() ,所以∠BEF=30°,得到∠AEF=60°,又因为AE=AF,得到∠FAE=60°,∠B=30°,然后利用扇形公式算出扇形FAE面积,用三角形ABE的面积减去扇形AEF面积即可
,所以∠BEF=30°,得到∠AEF=60°,又因为AE=AF,得到∠FAE=60°,∠B=30°,然后利用扇形公式算出扇形FAE面积,用三角形ABE的面积减去扇形AEF面积即可
(1)证明:作AH⊥CD于H,连结AE,AC,如图,
∵BC与⊙A相切于点E,
∴AE⊥BC,
∵四边形ABCD为菱形,
∴AC平分∠BCD,
而AE⊥BC,AH⊥CD,
∴AE=AH,
即CD为⊙A的半径,
∴⊙A与边CD也相切;
(2)解:∵tan∠BEF=![]() ,
,
∴∠BEF=30°,
∵∠AEB=90°,
∴∠AEF=60°,
∵AE=AF,
∴∠FAE=60°,∠B=30°,
∵AE=2,
∴S扇形FAE=![]() ,BE=
,BE=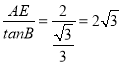
∴S阴影=S△ABE﹣S扇形AEF=![]() ×2×2
×2×2![]() ﹣
﹣![]() π=2
π=2![]() ﹣
﹣![]() π.
π.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.
(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;
(2)如果AC=1,tan∠B=![]() ,求∠CAD的正弦值.
,求∠CAD的正弦值.
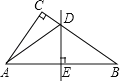
查看答案和解析>>
科目:初中数学 来源: 题型:
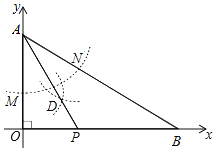
【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A. (1,0)B. (![]() ,0)C. (
,0)C. (![]()
![]() ,0)D. (2
,0)D. (2![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对排球、羽毛球、足球、篮球(以下分别用A、B、C、D表示)这四种球类运动的喜好情况.对全体学生进行了抽样调查(每位学生只能选一项最喜欢的运动),并将调查情况绘制成如下两幅不完整的统计图.
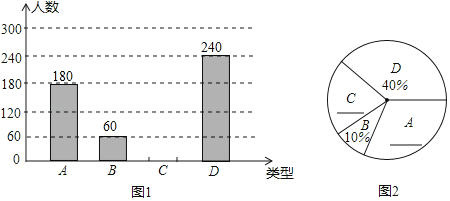
请根据以上信息回答下面问题:
(1)本次参加抽样调查的学生有 人.
(2)补全两幅统计图.
(3)若从本次参加抽样调查的学生中任取1人,则此人喜欢哪类球的概率最大?求其概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,无人飞机从A点水平飞行10秒至B点,在地面上C处测得A点、B点的仰角分别为45°,75°,已知无人飞机的飞行速度为80米/秒,则这架无人飞机的飞行高度为_____.
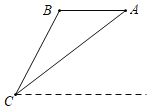
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
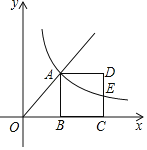
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有
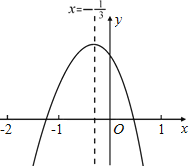
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
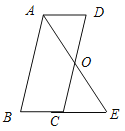
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com