
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.
(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;
(2)如果AC=1,tan∠B=![]() ,求∠CAD的正弦值.
,求∠CAD的正弦值.
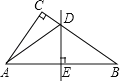
【答案】(1)∠CAD=18°;(2)∠CAD的正弦值为![]() .
.
【解析】
(1)由DE垂直平分AB交边BC、AB于点D、E,可得∠DAB=∠DBA,则∠CAD+∠DAB+∠DBA=∠CAD+2∠DAB=90°,而∠CAD:∠DAB=1:2,则可求∠CAD的度数.
(2)在Rt△ABC中,AC=1,tan∠B=![]() ,可求得BC,从而利用勾股定理可求得AB的值,进而可求得AE、DE的值,即可求得AD,而cos∠CAD=
,可求得BC,从而利用勾股定理可求得AB的值,进而可求得AE、DE的值,即可求得AD,而cos∠CAD=![]() ,sin∠CAD=
,sin∠CAD=![]() ,即可求∠CAD的正弦值.
,即可求∠CAD的正弦值.
(1)∵∠CAD:∠DAB=1:2
∴∠DAB=2∠CAD
在Rt△ABC中,∠CAD+∠DAB+∠DBA=90°
∵DE垂直平分AB交边BC、AB于点D、E
∴∠DAB=∠DBA
∴∠CAD+∠DAB+∠DBA=∠CAD+2∠CAD+2∠CAD=90°
解得,∠CAD=18°
(2)在Rt△ABC中,AC=1,tan∠B=![]() ,
,
∴BC=2
由勾股定理得,AB=![]()
∵DE垂直平分AB交边BC、AB于点D、E
∴BE=AE=![]()
∵∠DAE=∠DBE
∴在Rt△ADE中
tan∠B=tan∠DAE=![]()
∴DE=![]()
∴由勾股定理得
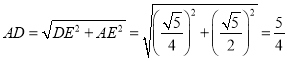 ∴cos∠CAD=
∴cos∠CAD=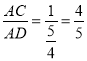
∴sin∠CAD=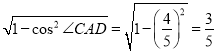
则∠CAD的正弦值为![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于两个点P,Q和图形W,如果在图形W上存在点M,N(M,N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.
(1)如图1,已知点A(0,3),B(2,3).
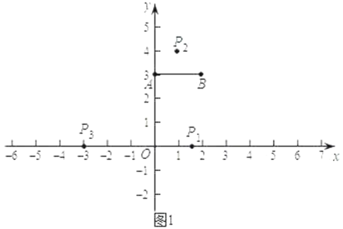
①设点O与线段AB上一点的距离为d,则d的最小值是 ,最大值是 ;
②在P1(![]() ,0),P2(1,4),P3(﹣3,0)这三个点中,与点O是线段AB的一对平衡点的是
,0),P2(1,4),P3(﹣3,0)这三个点中,与点O是线段AB的一对平衡点的是
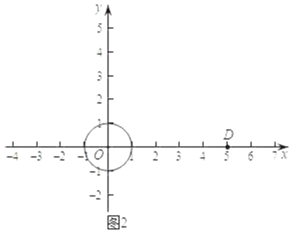
(2)如图2,已知圆O的半径为1,点D的坐标为(5,0),若点E(x,2)在第一象限,且点D与点E是圆O的一对平衡点,求x的取值范围.
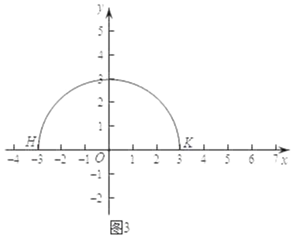
(3)如图3,已知点H(﹣3,0),以点O为圆心,OH长为半径画弧交x轴的正半轴于点K,点C(a,b)(其中b≥0)是坐标平面内一个动点,且OC=5,圆C是以点C为圆心,半径为2的圆,若弧HK上的任意两个点都是圆C的一对平衡点,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
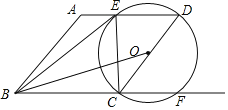
【题目】如图,在菱形ABCD中,取CD中点O,以O为圆心OD为半径作圆交AD于E交BC的延长线交于点F,AB=4,BE=5,连结OB
(1)求DE的长;
(2)求tan∠OBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:

①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系,根据图象,下列说法正确的是( )
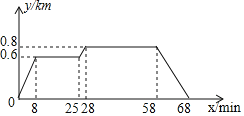
A.小明吃早餐用了25min
B.食堂到图书馆的距离为0.6km
C.小明读报用了30min
D.小明从图书馆回家的速度为0.8km/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
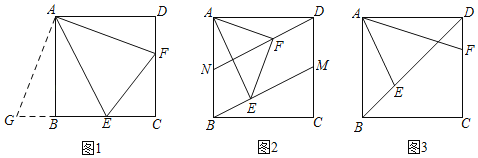
【题目】已知,正方形ABCD,∠EAF=45°,
(1)如图1,当点E,F分别在边BC,CD上,连接EF,求证:EF=BE+DF;
(2)如图2,点M,N分别在边AB,CD上,且BN=DM,当点E,F分别在BM,DN上,连接EF,请探究线段EF,BE,DF之间满足的数量关系,并加以证明;
(3)如图3,当点E,F分别在对角线BD,边CD上,若FC=2,则BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
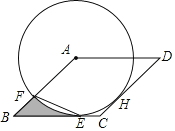
【题目】如图,已知⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连接EF.
(1)求证:CD是⊙A的切线;
(2)若⊙A的半径为2,tan∠BEF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com