
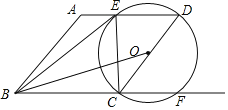
【题目】如图,在菱形ABCD中,取CD中点O,以O为圆心OD为半径作圆交AD于E交BC的延长线交于点F,AB=4,BE=5,连结OB
(1)求DE的长;
(2)求tan∠OBC的值.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
(1)根据菱形的性质得到AB=BC=CD=4,AD∥BC,根据圆周角定理得到∠DEC=90°,根据勾股定理即可得到结论;
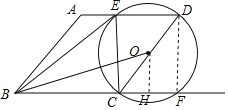
(2)连接DF,过O作OH⊥CF于H,推出四边形ECFD是矩形,得到DF=CE=3,CF=DE=![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=4,AD∥BC,
∵CD是⊙O的直径,
∴∠DEC=90°,
∴∠BCE=∠DEC=90°,
∴CE=![]() =3,
=3,
∴DE=![]() ;
;
(2)连接DF,过O作OH⊥CF于H,
∵CD是⊙O的直径,
∴∠DFC=90°,
∴四边形ECFD是矩形,
∴DF=CE=3,CF=DE=![]() ,
,
∴CH=![]() ,
,
∴OH=![]() DF=
DF=![]() ,
,
∴BH=BC+CH=![]() ,
,
∴tan∠OBC=![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
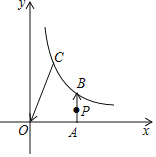
【题目】如图,点A在x轴上,点B,C在反比例函数y=![]() (k>0,x>0)的图象上.有一个动点P从点A出发,沿A→B→C→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴,垂足为M,设△POM的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
(k>0,x>0)的图象上.有一个动点P从点A出发,沿A→B→C→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴,垂足为M,设△POM的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 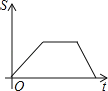 B.
B. 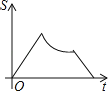
C. 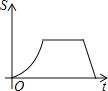 D.
D. 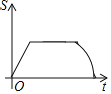
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC和△DBE均为等腰直角三角形,其中∠ABC=90°,∠DBE=90°.

(1)求证:AD=CE;
(2)求证:AD和CE垂直.
查看答案和解析>>
科目:初中数学 来源: 题型:
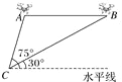
【题目】某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的地方,图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h;
③小明从甲地去乙地来回过程中,两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为( )
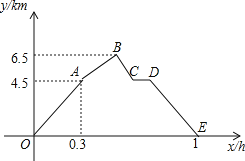
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
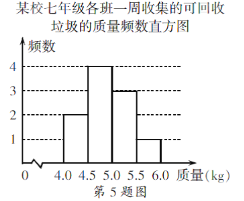
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为10cm2,BP平分∠ABC,AP⊥BP,垂足为P,连接CP,若三角形内有一点M,则点M落在△BPC内(包括边界)的概率为_____.
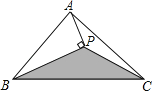
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.
(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;
(2)如果AC=1,tan∠B=![]() ,求∠CAD的正弦值.
,求∠CAD的正弦值.
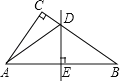
查看答案和解析>>
科目:初中数学 来源: 题型:
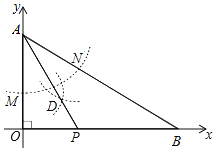
【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A. (1,0)B. (![]() ,0)C. (
,0)C. (![]()
![]() ,0)D. (2
,0)D. (2![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com