
【题目】已知,正方形ABCD,∠EAF=45°,
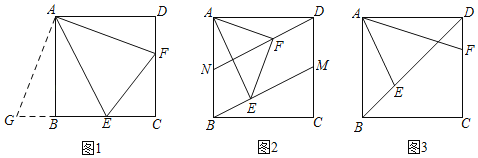
(1)如图1,当点E,F分别在边BC,CD上,连接EF,求证:EF=BE+DF;
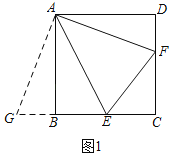
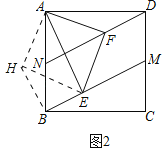
(2)如图2,点M,N分别在边AB,CD上,且BN=DM,当点E,F分别在BM,DN上,连接EF,请探究线段EF,BE,DF之间满足的数量关系,并加以证明;
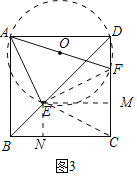
(3)如图3,当点E,F分别在对角线BD,边CD上,若FC=2,则BE的长为 .
【答案】(1)见解析;(2)EF2=BE2+DF2 ;理由见解析;(3)![]()
【解析】
(1)如图1中,将△ADF绕点A顺时针旋转90°,得△ABG,想办法证明△EAG≌△EAF(SAS).
(2)结论:EF2=BE2+DF2,将△ADF绕点A顺时针旋转90°,得△ABH,(如图2)证明过程跟(1)类似,证得△EAH≌△EAF,把EF转化到EH,然后利用BN=DM证明四边形BMDN为平行四边形得∠ABE=∠FDM,得∠EBH=∠ABH+∠ABE=∠ADF+∠MDN=90°,由EH2=BE2+BH2得EF2=BE2+DF2.
(3)作△ADF的外接圆⊙O,连接EF、EC,过点E分别作EM⊥CD于M,EN⊥BC于N(如图3).想办法证明EF=FC,即可推出封门村吗,证明EN=CM即可.
(1)证明:如图1中,将△ADF绕点A顺时针旋转90°,得△ABG,
∴△ADF≌△ABG,
∴AF=AG,DF=BG,∠DAF=∠BAG,
∵正方形ABCD,
∴∠D=∠BAD=∠ABE=90°,AB=AD,
∴∠ABG=∠D=90°,即G、B、C在同一直线上,
∵∠EAF=45°,
∴∠DAF+∠BAE=90°﹣45°=45°,
∴∠EAG=∠BAG+∠BAE=∠DAF+∠BAE=45°,
即∠EAG=∠EAF,
∴△EAG≌△EAF(SAS),
∴EG=EF,
∵BE+DF=BE+BG=EG,
∴EF=BE+DF.
(2)结论:EF2=BE2+DF2,
理由:将△ADF绕点A顺时针旋转90°,得△ABH,(如图2)
∴△ADF≌△ABH,
∴AF=AH,DF=BH,∠DAF=∠BAH,∠ADF=∠ABH,
∵∠EAF=45°,
∴∠DAF+∠BAE=90°﹣45°=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=45°,
即∠EAH=∠EAF,
∴△EAH≌△EAF(SAS),
∴EH=EF,
∵BN=DM,BN∥DM,
∴四边形BMDN是平行四边形,
∴∠ABE=∠MDN,
∴∠EBH=∠ABH+∠ABE=∠ADF+∠MDN=∠ADM=90°,
∴EH2=BE2+BH2,
∴EF2=BE2+DF2,
(3)作△ADF的外接圆⊙O,连接EF、EC,过点E分别作EM⊥CD于M,EN⊥BC于N(如图3).
∵∠ADF=90°,
∴AF为⊙O直径,
∵BD为正方形ABCD对角线,
∴∠EDF=∠EAF=45°,
∴点E在⊙O上,
∴∠AEF=90°,
∴△AEF为等腰直角三角形,
∴AE=EF,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∴CE=EF,
∵EM⊥CF,CF=2,
∴CM=![]() CF=1,
CF=1,
∵EN⊥BC,∠NCM=90°,
∴四边形CMEN是矩形
∴EN=CM=1,
∵∠EBN=45°,
∴BE=![]() EN=
EN=![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
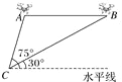
【题目】某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
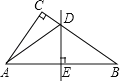
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.
(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;
(2)如果AC=1,tan∠B=![]() ,求∠CAD的正弦值.
,求∠CAD的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读有助于提高孩子的学习兴趣和积极性,但近年来出现很多中学生在学校看武侠小说的现象,某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生在校看武侠小说”这一现象的看法,统计整理并制作了如下的条形与扇形统计图.依据图中信息,解答下列问题:
(1)本次调查的学生家长有 名,“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是 ;
(2)请补全条形统计图(标上柱高数值);
(3)该学校共3000名学生家长,请估计该校抱“不赞同”态度的学生家长人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
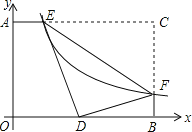
【题目】如图,反比例函数![]() 的图象与矩形AOBC的边AC,BC分别相交于点E,F,点C的坐标为(4,3)将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
的图象与矩形AOBC的边AC,BC分别相交于点E,F,点C的坐标为(4,3)将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
A. ![]() B. 6C. 3D.
B. 6C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
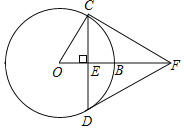
【题目】如图,点B是⊙O上一点,弦CD⊥OB于点E,过点C的切线交OB的延长线于点F,连接DF,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为2,∠CFD=60°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
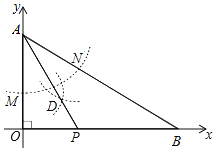
【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A. (1,0)B. (![]() ,0)C. (
,0)C. (![]()
![]() ,0)D. (2
,0)D. (2![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对排球、羽毛球、足球、篮球(以下分别用A、B、C、D表示)这四种球类运动的喜好情况.对全体学生进行了抽样调查(每位学生只能选一项最喜欢的运动),并将调查情况绘制成如下两幅不完整的统计图.
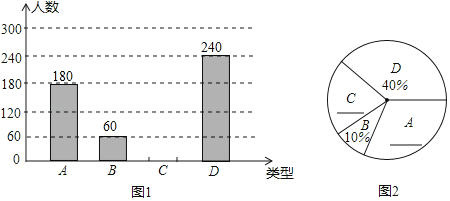
请根据以上信息回答下面问题:
(1)本次参加抽样调查的学生有 人.
(2)补全两幅统计图.
(3)若从本次参加抽样调查的学生中任取1人,则此人喜欢哪类球的概率最大?求其概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
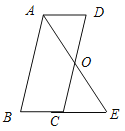
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com