
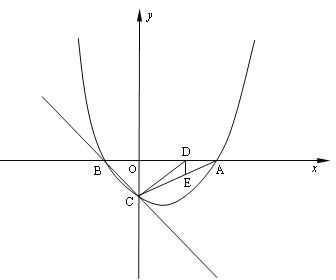
【题目】如图, 已知抛物线![]() 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由.
【答案】(1) y=![]() x2-
x2-![]() x-1;(2) D(1,0);(3) P1(2.5,-3.5)、P2(1,-2)、P3(
x-1;(2) D(1,0);(3) P1(2.5,-3.5)、P2(1,-2)、P3(![]() ,-
,-![]() -1),P4(-
-1),P4(-![]() ,
,![]() -1).
-1).
【解析】
(1)用待定系数法求得二次函数的解析式;
(2)设点D的坐标为(m,0), (0<m<2),由△ADE∽△AOC得,![]() 从而求得DE的长,通过△CDE的面积公式求得当m=1时,△CDE的面积最大,即可求出点D的坐标;
从而求得DE的长,通过△CDE的面积公式求得当m=1时,△CDE的面积最大,即可求出点D的坐标;
(3)求出直线BC的解析式,若三角形为等腰三角形,则有三种可能,利用勾股定理从而求得P点的坐标.
解:(1)∵二次函数![]() 的图像经过点A(2,0)C(0,-1)
的图像经过点A(2,0)C(0,-1)
∴![]()
![]() 解得:b=-
解得:b=-![]() c=-1
c=-1
∴二次函数的解析式为![]()
(2)设点D的坐标为(m,0), (0<m<2)
∴ OD=m∴AD=2-m由△ADE∽△AOC得,![]()
∴![]() ∴DE=
∴DE=![]()
∴△CDE的面积=![]() ×
×![]() ×m=
×m=![]()
![]()
当m=1时,△CDE的面积最大,此时点D的坐标为(1,0)
(3)存在.
由(1)知:二次函数的解析式为![]()
设y=0则![]() 解得:x1=2, x2=-1
解得:x1=2, x2=-1![]() ,
,
∴点B的坐标为(-1,0) C(0,-1)
设直线BC的解析式为:y=kx+b
∴![]() 解得:k=-1,b=-1,
解得:k=-1,b=-1,
∴直线BC的解析式为:y=-x-1
在Rt△AOC中,∠AOC=90°
OA=2 OC=1,由勾股定理得:AC=![]()
∵点B(-1,0) 点C(0,-1),∴OB=OC ∠BCO=45°
①当以点C为顶点且PC=AC=![]() 时,
时,
设P(k, -k-1),过点P作PH⊥y轴于H,
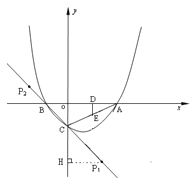
∴∠HCP=∠BCO=45°,CH=PH=∣k∣,在Rt△PCH中
k2+k2=![]() 解得k1=
解得k1=![]() ,k2=-
,k2=-![]()
∴P1(![]() ,-
,-![]() ) P2(-
) P2(-![]() ,
,![]() )
)
②以A为顶点,即AC=AP=![]()
设P(k, -k-1),过点P作PG⊥x轴于G,
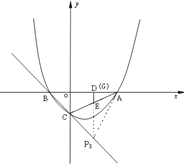
AG=∣2-k∣ GP=∣-k-1∣
在Rt△APG中 AG2+PG2=AP2,(2-k)2+(-k-1)2=5 解得:k1=1,k2=0(舍)
∴P3(1, -2) (3分)
(3)AP=CP,此时AP=CP
2x-2x+5=2x
-2x=-5,x=2.5
代入BC方程,y=-3.5
因此P4(2.5,-3.5)
综上所述,存在四点:P1(2.5,-3.5)、P2(1,-2)、P3(,-
![]() -1),P4(-
-1),P4(-![]() ,
,![]() -1).
-1).


科目:初中数学 来源: 题型:
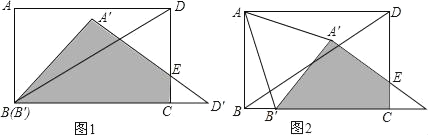
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() ,将
,将![]() 绕
绕![]() 点作顺时针方向旋转得到
点作顺时针方向旋转得到![]() (
(![]() 与
与![]() 重合),且点
重合),且点![]() 刚好落在
刚好落在![]() 的延长上,
的延长上,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求矩形![]() 与
与![]() 重叠部分(如图1中阴影部分
重叠部分(如图1中阴影部分![]() )的面积;
)的面积;
(2)将![]() 以每秒2
以每秒2![]() 的速度沿直线
的速度沿直线![]() 向右平移,如图2,当
向右平移,如图2,当![]() 移动到
移动到![]() 点时停止移动.设矩形
点时停止移动.设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,移动的时间为
,移动的时间为![]() ,请你直接写出
,请你直接写出![]() 关于
关于![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的平移过程中,是否存在这样的时间![]() ,使得
,使得![]() 成为等腰三角形?若存在,请你直接写出对应的
成为等腰三角形?若存在,请你直接写出对应的![]() 的值,若不存在,请你说明理由.
的值,若不存在,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
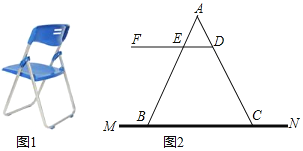
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
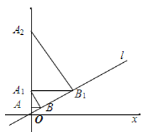
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
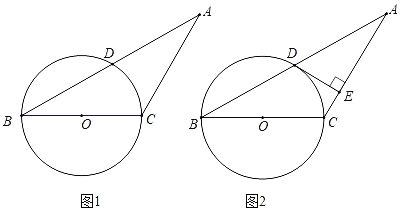
(1)求证:点D是AB的中点;
(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com