
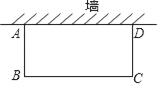
【题目】某农场要建一个长方形ABCD的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m.
(1)若养鸡场面积为168m2,求鸡场垂直于墙的一边AB的长.
(2)请问应怎样围才能使养鸡场面积最大?最大的面积是多少?
【答案】(1)鸡场垂直于墙的一边AB的长为14米;(2)鸡场垂直于墙的一边AB的长为10米时,围成养鸡场面积最大,最大值200米2.
【解析】试题分析:(1)首先设鸡场垂直于墙的一边AB的长为x 米,然后根据题意可得方程x(40-2x)=168,即可求得x的值,又由墙长25m,可得x=14,则问题得解;
(2)设围成养鸡场面积为S,由题意可得S与x的函数关系式,由二次函数最大值的求解方法即可求得答案;
解:(1)设鸡场垂直于墙的一边AB的长为x米,
则 x(40﹣2x)=168,
整理得:x2﹣20x+84=0,
解得:x1=14,x2=6,
∵墙长25m,
∴0≤BC≤25,即0≤40﹣2x≤25,
解得:7.5≤x≤20,
∴x=14.
答:鸡场垂直于墙的一边AB的长为14米.
(2)围成养鸡场面积为S米2,
则S=x(40﹣2x)
=﹣2x2+40x
=﹣2(x2﹣20x)
=﹣2(x2﹣20x+102)+2×102
=﹣2(x﹣10)2+200,
∵﹣2(x﹣10)2≤0,
∴当x=10时,S有最大值200.
即鸡场垂直于墙的一边AB的长为10米时,围成养鸡场面积最大,最大值200米2.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=54°,AD是△ABC的角平分线.求作AB的垂直平分线MN交AD于点E,连接BE;并证明DE=DB.(要求:尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
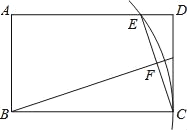
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x﹣2分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x﹣2分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=![]() (x<0)的图象于点D,且OD∥AB.
(x<0)的图象于点D,且OD∥AB.
(1)求k的值;
(2)连接OP、AD,求证:四边形APOD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解满足x为非正数,y为负数.
的解满足x为非正数,y为负数.
(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.
查看答案和解析>>
科目:初中数学 来源: 题型:
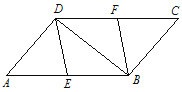
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遂宁骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3万元,今年经过改造升级后A型车每辆销售价比去年增加300元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加20%.
(1)求今年2月份A型车每辆销售价多少元?
(2)该车行计划今年3月份新进一批A型车和B型车共40辆,且B型车的进货数量不超过A型车数量的2倍,A、B两种型号车的进货和销售价格如表,问应如何进货才能使这批车获利最多?
A型车 | B型车 | |
进货价格(元/辆) | 900 | 1000 |
销售价格(元/辆) | 今年的销售价格 | 2000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com