练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某小组在一次“在线测试”中做对的题数分别是10，8，6，9，8，7，8，对于这组数据，下列判断中错误的是（ ）

    A.众数是8B.中位数是8C.平均数是8D.方差是8

    【答案】D

    【解析】

    由题意可知：这组数据的平均数＝（10+8+6+9+8+7+8）÷7；总数个数是奇数的，按从小到大的顺序排列，取中间的那个数便为中位数，按此方法求中位数；一组数据中，出现次数最多的数就叫这组数据的众数，这组数据8出现次数最多，由此求出众数；一组数据中各数据与这组数据的平均数的差的平方的平均数叫做这组数据的方差，按此方法计算方差．

    解：平均数＝（10+8+6+9+8+7+8）÷7＝8；

    按从小到大排列为：6，7，8，8，8，9，10，

    ∴中位数是8；

    ∵8出现了3次，次数最多，

    ∴众数是8；

    方差S2＝[（10﹣8）2+（8﹣8）2+（6﹣8）2+（9﹣8）2+（8﹣8）2+（7﹣8）2+（8﹣8）2]＝1.25．

    所以D错误．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（3分）如图，在等边△ABC中，AB=10，BD=4，BE=2，点P从点E出发沿EA方向运动，连接PD，以PD为边，在PD右侧按如图方式作等边△DPF，当点P从点E运动到点A时，点F运动的路径长是（ ）

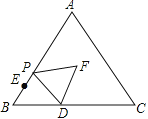
    A. 8 B. 10 C. 3π D. 5π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020春开学为防控冠状病毒，学生进校园必须戴口罩，测体温，江阴初级中学开通了三条人工测体温的通道，每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温(每个通道一位老师)，周一有小卫和小孙两学生进校园，在3个人工测体温通道中，可随机选择其中的一个通过．

    (1) 求小孙进校园时，由王老师测体温的概率；

    (2)求两学生进校园时，都是王老师测体温的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．

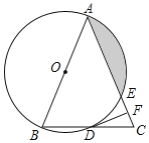
    （1）求证：直线DF是⊙O的切线；

    （2）求证：BC2＝4CFAC；

    （3）若⊙O的半径为4，∠CDF＝15°，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，现有一横截面是一抛物线的水渠．一次，水渠管理员将一根长的标杆一端放在水渠底部的点，另一端露出水面并靠在水渠边缘的点，发现标杆有浸没在水中，露出水面部分的标杆与水面成的夹角（标杆与抛物线的横截面在同一平面内）．

    （1）以水面所在直线为轴，建立如图所示的直角坐标系，求该水渠横截面抛物线的解析式（结果保留根号）；

    （2）在（1）的条件下，求当水面再上升时的水面宽约为多少？（取，结果精确到）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“停课不停学”期间，小明用电脑在线上课，图1是他的电脑液晶显示器的侧面图，显示屏AB可以绕O点旋转一定角度．研究表明：当眼睛E与显示屏顶端A在同一水平线上，且望向显示器屏幕形成一个18°俯角（即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP）时，对保护眼睛比较好，而且显示屏顶端A与底座C的连线AC与水平线CD垂直时（如图2）时，观看屏幕最舒适，此时测得∠BCD＝30°，∠APE＝90°，液晶显示屏的宽AB为32cm．

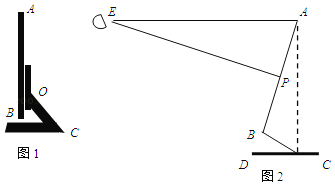
    （1）求眼睛E与显示屏顶端A的水平距离AE；（结果精确到1cm）

    （2）求显示屏顶端A与底座C的距离AC．（结果精确到1cm）（参考数据：sin18°≈0.3，cos18°≈0.9，tan18°≈0.3，≈1.4，≈1.7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论： ①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1 ，

    其中正确的是________．

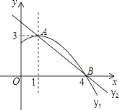
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知网格的小正方形的边长均为1，格点三角形ABC如图所示，请用没有刻度的直尺画出满足条件的图形

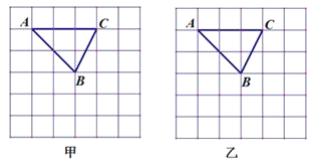
    （1）在甲图中，画出△，且相似比为2：1，各顶点都在格点上．

    （2）在乙图中，把线段AB三等分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出

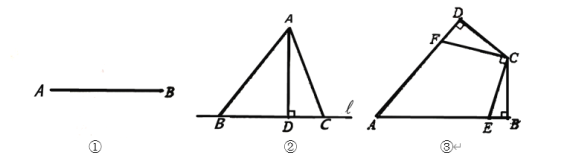
    （1）如图①，已知线段AB，请以AB为斜边，在图中画出一个直角三角形；

    （2）如图②，已知点A是直线l外一点，点B、C均在直线l上，AD⊥l且AD=3，∠BAC=60°，求△ABC面积的最小值；

    问题解决

    （3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD中，∠A=45°，∠B=∠D=90°，CB=CD=6m，点E、F分别为AB、AD上的点，若保持CE⊥CF，那么四边形AECF的面积是否存在最大值?若存在，请求出面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案