
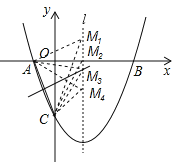
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
【答案】(1)![]() ;(2)P(1,0);(3).
;(2)P(1,0);(3).
【解析】
试题(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A.B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l与x轴的交点,即为符合条件的P点;
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
试题解析:(1)将A(﹣1,0)、B(3,0)、C(0,﹣3)代入抛物线![]() 中,得:
中,得: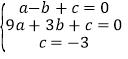 ,解得:
,解得: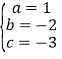 ,故抛物线的解析式:
,故抛物线的解析式:![]() .
.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,此时x=![]() =1,故P(1,0);
=1,故P(1,0);
(3)如图所示:抛物线的对称轴为:x=![]() =1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
=1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =10;
=10;
①若MA=MC,则![]() ,得:
,得:![]() =
=![]() ,解得:m=﹣1;
,解得:m=﹣1;
②若MA=AC,则![]() ,得:
,得:![]() =10,得:m=
=10,得:m=![]() ;
;
③若MC=AC,则![]() ,得:
,得:![]() =10,得:
=10,得:![]() ,
,![]() ;
;
当m=﹣6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,![]() )(1,
)(1,![]() )(1,﹣1)(1,0).
)(1,﹣1)(1,0).


科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
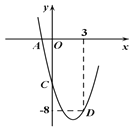
【题目】二次函数![]() 的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).(1)求此二次函数的解析式; (2)用配方法将将此二次函数的解析式写成
的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).(1)求此二次函数的解析式; (2)用配方法将将此二次函数的解析式写成![]() 的形式,并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
的形式,并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
是关于的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求![]() 的值;
的值;
(2)若![]() 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P与图形W,若点Q为图形W上任意一点,点Q关于第一、三象限角平分线的对称点为Q,且线段PQ,的中点为M(m,0),则称点P是图形W关于点M(m,0)的“关联点”.
(1)如图1,若点P是点Q(0,![]() )关于原点的关联点,则点P的坐标为 ;
)关于原点的关联点,则点P的坐标为 ;
(2)如图2,在△ABC中,A(2,2),B(-2,0),C(0,-2),
①将线段AO向右平移d(d>0)个单位长度,若平移后的线段上存在两个△ABC关于点(2,0)的关联点,则d的取值范围是 .
②已知点S(n+2,0)和点T(n+4,0),若线段ST上存在△ABC关于点N(n,0)的关联点,求n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雪枫中学是亳州市精细化管理示范校,量化管理充分调动学生的学习热情,某班为了鼓励学生周末在家做试卷,规定每人每月做试卷不超过5张的,在月底量化考核中每人每张加2分;超过5张的部分,每人每张加3分,另外对超过5张的学生由班主任再额外一次性奖励1.5分。设小明这个月做x张,本月量化总得分为y分.
(1)试写出总分y (分)与x (张)之间的函数关系式:
(2)如果小明本学期9月份做了8张试卷,那他总共得了多少分?
(3)如果小明本学期10月份量化得41.5分,那么他做了多少张试卷?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com