
分析 (1)设买大枣粽子x元/盒,普通粽子y元/盒,根据两种粽子的单价和购买两种粽子用300元列出二元一次方程组,然后求解即可;
(2)①表示出购买普通粽子的(20-x)盒,然后根据购买水果的钱数等于善款总数减去购买两种粽子的钱数,整理即可得解;
②根据购买水果的钱数不少于180元但不超过240元列出不等式组,然后求解得到x的取值范围,再根据粽子的盒数是正整数从而写出所有的可能购买方案,再根据一次函数的增减性求出购买水果钱数最多的方案.
解答 解:(1)设买大枣粽子x元/盒,普通粽子y元/盒,
根据题意得,$\left\{\begin{array}{l}{x-y=15}\\{2x+4y=300}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=60}\\{y=45}\end{array}\right.$,
答:大枣粽子60元/盒,普通粽子45元/盒;
(2)①设买大枣粽子x盒,则购买普通粽子(20-x)盒,买水果共用了w元,
根据题意得,w=1240-60x-45(20-x),
=1240-60x-900+45x,
=-15x+340,
故,w关于x的函数关系式为w=-15x+340;
②∵要求购买水果的钱数不少于180元但不超过240元,
∴$\left\{\begin{array}{l}{-15x+340≥180①}\\{-15x+340≤240②}\end{array}\right.$,
解不等式①得,x≤10$\frac{2}{3}$,
解不等式②得,x≥6$\frac{2}{3}$,
所以,不等式组的解集是6$\frac{2}{3}$≤x≤10$\frac{2}{3}$,
∵x是正整数,
∴x=7、8、9、10,
可能方案有:
方案一:购买大枣粽子7盒,普通粽子13盒,
方案二:购买大枣粽子8盒,普通粽子12盒,
方案三:购买大枣粽子9盒,普通粽子11盒,
方案四:购买大枣粽子10盒,普通粽子10盒;
∵-15<0,
∴w随x的增大而减小,
∴方案一可使购买水果的钱数最多,最多为-15×7+340=235元.
点评 本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.


科目:初中数学 来源: 题型:解答题
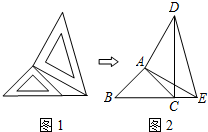 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
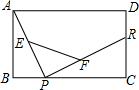 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )| A. | 线段EF的长逐渐增大 | B. | 线段EF的长逐渐减少 | ||
| C. | 线段EF的长不变 | D. | 线段EF的长先增大后变小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
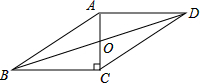 如图,在?ABCD中,AB=10,AD=8,AC⊥BC,下列计算错误的是( )
如图,在?ABCD中,AB=10,AD=8,AC⊥BC,下列计算错误的是( )| A. | BC=8 | B. | BD=15 | C. | AC=6 | D. | ?ABCD的面积是48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com