
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

【答案】(1)证明见解析;(2)![]() -8.
-8.
【解析】试题分析:(1)连接AD、OD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,所以OD∥AC,则DF⊥OD,然后根据切线的判定定理可得DF是⊙O的切线;
(2)利用S阴影=S扇形AOE-S△AOE进而求出答案.
试题解析:(1)连接AD,OD.
∵AB是直径,
∴∠ADB=90°,∴AD⊥BC.
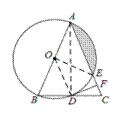
∵AB=AC ,
∴D是BC的中点.
∵O是AB的中点,
∴OD//AC.
∴∠ODF+∠DFA=180°
∵DF⊥AC,∴∠DFA=90°.
∴∠ODF=90°. ∴OD⊥DF
∴DF是⊙O的切线.
(2)连接OE
∵∠ADB=∠ADC=90°,∠DFC=∠DFA=90°,
∴∠DAC=∠CDF=22.5°
∵AB=AC,D是BC中点,
∴∠BAC=2∠DAC=2×22.5°=45°.
∵OA=OE,
∴∠OEA=∠BAC=45°.
∴∠AOE=90° .
∵AE=4![]() ,
,
∴OA=OE=4.
S阴影=S扇形AOE-S△AOE=4π-8.


科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧![]() 的中点,点D是优弧
的中点,点D是优弧![]() 上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=
上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=![]() cm;③cos∠AOB=
cm;③cos∠AOB=![]() ;④四边形ABOC是菱形. 其中正确结论的序号是( )
;④四边形ABOC是菱形. 其中正确结论的序号是( )

A. ①③ B. ①②③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线: ![]() .
.
(1)求抛物线的顶点坐标.
(2)若直线![]() 经过(2,0)点且与
经过(2,0)点且与![]() 轴垂直,直线
轴垂直,直线![]() 经过抛物线的顶点与坐标原点,且
经过抛物线的顶点与坐标原点,且![]() 与
与![]() 的交点P在抛物线上.求抛物线的表达式.
的交点P在抛物线上.求抛物线的表达式.
(3)已知点A(0,2),点A关于![]() 轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出
轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.

(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的爸爸去参加一个重要会议,小明坐在汽车上用所学知识绘制了一张反映小车速度与时间的关系图,第二天,小明拿着这张图给同学看,并向同学提出如下问题,你能回答吗?

(1)在上述变化过程中,图象表示了那两个变量的关系?哪个是自变量?哪个是因变量?
(2)小车共行驶了多少时间?最高时速是什么?停止了几分钟?
(3)小车在哪段时间保持匀速行驶?匀速行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,
,![]() .
.

(1)若![]() 是
是![]() 的高线,且
的高线,且![]() ,求
,求![]() 的长.
的长.

(2)若![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求出
,求出![]() 的面积.
的面积.

(3)填空:若![]() 是
是![]() 的中线,设
的中线,设![]() 长为
长为![]() ,则
,则![]() 的取值范围______.
的取值范围______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=![]() AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )
AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
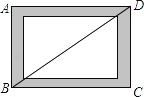
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com