
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.

(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
【答案】(1)1;(2)证明详见解析;(3)![]() ≤OD≤2.
≤OD≤2.
【解析】
试题分析:(1)画出图形,根据DE垂直平分BC,可得出DE是△BOA的中位线,从而利用中位线的性质求出DE的长度;
(2)先根据中垂线的性质得出DB=DC,EB=EC,然后结合CE∥OB判断出BE∥DC,得出四边形BDCE为平行四边形,结合DB=DC可得出结论.
(3)求两个极值点,①当点C与点A重合时,OD取得最小值,②当点C与点O重合时,OD取得最大值,继而可得出OD的取值范围.
试题解析:解:∵直线AB的解析式为y=﹣2x+4,
∴点A的坐标为(2,0),点B的坐标为(0,4),即可得OB=4,OA=2,
(1)当点C与点O重合时如图所示,

∵DE垂直平分BC(BO),
∴DE是△BOA的中位线,
∴DE=![]() OA=1;
OA=1;
(2)当CE∥OB时,如图所示:

∵DE为BC的中垂线,
∴BD=CD,EB=EC,
∴∠DBC=∠DCB,∠EBC=∠ECB,
∴∠DCE=∠DBE,
∵CE∥OB,
∴∠CEA=∠DBE,
∴∠CEA=∠DCE,
∴BE∥DC,
∴四边形BDCE为平行四边形,
又∵BD=CD,
∴四边形BDCE为菱形.
(3)当点C与点O重合时,OD取得最大值,此时OD=![]() OB=2;
OB=2;
当点C与点A重合时,OD取得最小值,如图所示:

在Rt△AOB中,AB=![]() =2
=2![]() ,
,
∵DE垂直平分BC(BA),
∴BE=![]() BA=
BA=![]() ,
,
易证△BDE∽△BAO,
∴![]() ,即
,即![]() ,
,
解得:BD=![]() ,
,
则OD=OB﹣BD=4﹣![]() =
=![]() .
.
综上可得:![]() ≤OD≤2.
≤OD≤2.


科目:初中数学 来源: 题型:
【题目】已知点O为数轴原点,点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,且|a+4|+(b﹣10)2=0.
![]()
(1)求线段AB的长;
(2)设点P在数轴上对应的数为x,当PA+PB=20时,求x的值;
(3)如图,M、N两点分别从O、B出发以v1、v2的速度同时沿数轴负方向运动(M在线段AO上,N在线段BO上),P是线段AN的中点,若M、N运动到任一时刻时,总有PM为定值,下列结论:①![]() 的值不变;②v1+v2的值不变.其中只有一个结论是正确的,请你找出正确的结论并求值.
的值不变;②v1+v2的值不变.其中只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月25日是第二十四个“全国中小学生安全教育日”,某校为加强学生的安全意识,以“防火、防溺水、防食物中毒、防校园欺凌”为主题组织了全校学生参加安全知识竞赛,从中抽取了部分学生成绩(得分为正整数,满分为100分)进行统计,绘制了两幅不完整的统计图,如图所示.
(1)学校共抽取了______名学生,![]() _____,n=______.
_____,n=______.
(2)补全频数直方图;
(3)该校共有2000名学生。若成绩在70分以下(含70分)的学生安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)求△ABC的面积为_______;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过点A(0,2)和B(-1,-4).
的图像经过点A(0,2)和B(-1,-4).

(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为![]() 的形式;
的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,点D与点A为对应点,画出Rt△ODC,并连接BC.
(1)填空:∠OBC=_____°;
(2)如图,连接AC,作OP⊥AC,垂足为P,求OP的长度是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
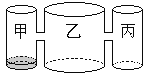
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com