
【题目】对于给定的两个“函数,任取自变量x的一个值,当x<1时,它们对应的函数值互为相反数;当x≥1时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x-4,它的相关函数为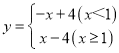 .
.
(1)一次函数y= -x+5的相关函数为______________.
(2)已知点A(b-1,4),点B坐标(b+3,4),函数y=3x-2的相关函数与线段AB有且只有一个交点,求b的取值范围.
(3)当b+1≤x≤b+2时,函数y=-3x+b-2的相关函数的最小值为3,求b的值.
【答案】(1)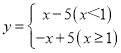 ;
;
(2)当x<1时,![]() ≤b≤
≤b≤![]() ;当x≥1时,
;当x≥1时,![]() ≤b≤
≤b≤![]() ;
;
(3)当x<1时,b=-1; 当x≥1时,b=-![]()
【解析】
(1)根据相关函数的概念可直接得出答案;
(2)由A(b-1,4),B(b+3,4)得到线段AB在直线y=4上,再求出y=3x-2的两个相关函数的图象与直线y=4的交点坐标,从而得到不等式,解不等式即可得出b的取值范围.
(3)分两种情况,当x<1时,y=-3x+b-2的相关函数是y=3x+2-b,根据一次函数的性质得到当x=b+1时,y有最小值为3,列出方程求解即可得出b值;同理,当x≥1时,y=-3x+b-2的相关函数是y=-3x+b-2, 由函数性质列出方程可得出b值.
解:(1)根据相关函数的概念可得,一次函数y= -x+5的相关函数为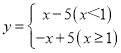 ;
;
(2)∵A(b-1,4),B(b+3,4),
∴线段AB在直线y=4上,且点A在点B的左边,
当x<1时,y=3x-2的相关函数是y=2-3x,
把y=4代入y=2-3x,得2-3x=4,解得x=-![]()
∴直线y=4与直线y=2-3x的交点的横坐标是x=-![]() ,
,
∴b-1≤-![]() ≤b+3
≤b+3
解得![]() ≤b≤
≤b≤![]()
当x≥1时,y=3x-2的相关函数是y=3x-2,
把y=4代入y=3x-2,得3x-2=4,解得x=2
∴直线y=4与直线y=3x-2的交点的横坐标是x=2,
∴b-1≤2≤b+3
解得![]() ≤b≤
≤b≤![]()
综上所述,当x<1时,![]() ≤b≤
≤b≤![]() ;当x≥1时,
;当x≥1时,![]() ≤b≤
≤b≤![]() .
.
(3)当x<1时,y=-3x+b-2的相关函数是y=3x+2-b,
∵k=3>0,y随x的增大而增大,
∵b+1≤x≤b+2
∴当x=b+1时,y有最小值为3
∴3(b+1)+2-b=3
解得b=-1;
当x≥1时,y=-3x+b-2的相关函数是y=-3x+b-2,
∵k=-3<0,y随x的增大而减小,
∵b+1≤x≤b+2
∴当x=b+2时,y有最小值为3
∴-3(b+2)+b-2=3
解得b=-![]()
综上,当x<1时,b=-1; 当x≥1时,b=-![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】以下是八(1)班学生身高的统计表和扇形统计图,请回答以下问题:
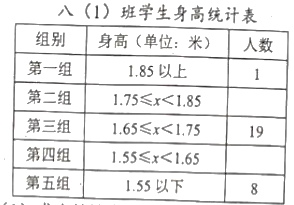
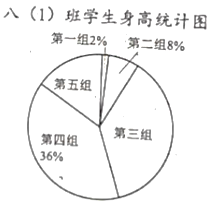
(1)求出统计表和统计图缺的数据.
(2)八(1)班学生身高这组数据的中位数落在第几组?
(3)如果现在八(1)班学生的平均身高是1.63m,已确定新学期班级转来两名新同学,新同学的身高分别是1.54m和1.77m,那么这组新数据的中位数落在第几组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
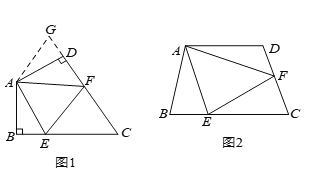
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.
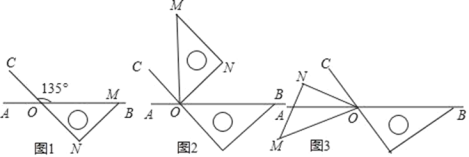
(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM= ;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第 秒时,∠COM与∠CON互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行年,乙乘坐汽车从A地出发沿同一路线匀速前往B地,甲先出发.设甲行驶的时间为x(h),甲、乙两人距出发点的路程S甲(km)、S乙(km)关于x的函数图象如图1所示,甲、乙两人之同的距离y(km)关于x的函数图象如图2所示,请你解决以下问题:
(1)甲的速度是__________km/h,乙的速度是_______km/h;
(2)a=_______,b=_______;
(3)甲出发多少时间后,甲、乙两人第二次相距7.5km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,tan∠ABC=![]() ,∠ACB=45°,AD=8,AD是边BC上的高,垂足为D,BE=4,点M从点B出发沿BC方向以每秒3个单位的速度运动,点N从点E出发,与点M同时同方向以每秒1个单位的速度运动.以MN为边在BC的上方作正方形MNGH.点M到达点C时停止运动,点N也随之停止运动.设运动时间为t(秒)(t>0).
,∠ACB=45°,AD=8,AD是边BC上的高,垂足为D,BE=4,点M从点B出发沿BC方向以每秒3个单位的速度运动,点N从点E出发,与点M同时同方向以每秒1个单位的速度运动.以MN为边在BC的上方作正方形MNGH.点M到达点C时停止运动,点N也随之停止运动.设运动时间为t(秒)(t>0).
(1)当t为多少秒时,点H刚好落在线段AB上?
(2)当t为多少秒时,点H刚好落在线段AC上?
(3)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,求出S关于t的函数关系式并写出自变量t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二青会开幕式期间,出租车司机李师傅营运时是在南北走向的滨河西路上行进的,如果规定向南为正,向北为负,他这天上午所接![]() 位乘客的行车里程(单位:
位乘客的行车里程(单位:![]() )为:
)为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(假设相邻两位乘客上下车没有时间间隔)
.(假设相邻两位乘客上下车没有时间间隔)
(1)试判断李师傅将最后一位乘客送到目的地时,他在出发点的什么方向,距离出发地多少千米?
(2)若汽车耗油量为![]() ,则这天上午李师傅接送乘客时出租车共耗油多少升?
,则这天上午李师傅接送乘客时出租车共耗油多少升?
(3)若出租车起步价为![]() 元,起步里程为
元,起步里程为![]() (包括
(包括![]() ),超过部分每千米
),超过部分每千米![]() 元,问李师傅这天上午共得车费多少元?
元,问李师傅这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com