
【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.
(1)求A,B,C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC,BC,若点E是线段AB上的一个动点(与点A,点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
【答案】
(1)解:解方程x2﹣10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=﹣2
∴由抛物线的对称性可得点A的坐标为(﹣6,0)
(2)解:∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(﹣6,0)、B(2,0)代入表达式,
得: ![]()
解得 
∴所求抛物线的表达式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+8
x+8
(3)解:依题意,AE=m,则BE=8﹣m,
∵OA=6,OC=8,
∴AC=10
∵EF∥AC
∴△BEF∽△BAC
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
∴EF= ![]() (6分)
(6分)
过点F作FG⊥AB,垂足为G,

则sin∠FEG=sin∠CAB= ![]()
∴ ![]() =
= ![]()
∴FG= ![]()
![]() =8﹣m
=8﹣m
∴S=S△BCE﹣S△BFE
= ![]() (8﹣m)×8﹣
(8﹣m)×8﹣ ![]() (8﹣m)(8﹣m)
(8﹣m)(8﹣m)
= ![]() (8﹣m)(8﹣8+m)
(8﹣m)(8﹣8+m)
= ![]() (8﹣m)m
(8﹣m)m
=﹣ ![]() m2+4m
m2+4m
自变量m的取值范围是0<m<8
(4)解:存在.
理由:∵S=﹣ ![]() m2+4m=﹣
m2+4m=﹣ ![]() (m﹣4)2+8且﹣
(m﹣4)2+8且﹣ ![]() <0,
<0,
∴当m=4时,S有最大值,S
∵m=4,
∴点E的坐标为(﹣2,0)
∴△BCE为等腰三角形.
【解析】(1)先解关于x的一元二次方程,得到线段OB、OC的长,从而可得到B、C两点坐标,根据抛物线的对称性可得点A坐标;
(2)把A、B、C三点代入二次函数解析式,得到关于a、b、c的方程组,从而可求得二次函数解析式;
(3)依据图形可得到S△EFF=S△BCE-S△BFE,从而可得到S与m的函数关系;
(4)利用二次函数求出最值,进而求得点E坐标.OC垂直平分BE,那么EC=BC,所求的三角形是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为迎接广州市青少年读书活动,某校倡议同学们利于课余时间多阅读为了解同学们的读书情况,在全校随机调查了部分同学在一周内的阅读时间,并用得到的数据绘制了统计图,根据图中信息解答下列问题:
![]() 被抽查学生阅读时间的中位数为多少小时,众数为多少小时,平均数为多少小时;
被抽查学生阅读时间的中位数为多少小时,众数为多少小时,平均数为多少小时;
![]() 已知全校学生人数为1500人,请你估算该校学生一周内阅读时间不少于三小时的有多少人?
已知全校学生人数为1500人,请你估算该校学生一周内阅读时间不少于三小时的有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A处与高楼的水平距离为60m,这栋高楼有多高?(结果精确到0.1m,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )
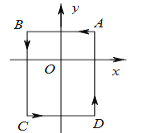
A. (-1,0)B. (1,2)C. (1,-1)D. (0,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:(1)a<O;(2)b2﹣4ac<0;(3)b>O;(4)a+b+c>0;(5)a﹣b+c>0.你认为其中正确信息的个数有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com