
【题目】(8分)热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A处与高楼的水平距离为60m,这栋高楼有多高?(结果精确到0.1m,参考数据:![]() )
)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点(
上任意一点(![]() 不与
不与![]() 重合),分别以
重合),分别以![]() 和
和![]() 为边在
为边在![]() 的下方作正方形
的下方作正方形![]() 和正方形
和正方形![]() ,以
,以![]() 和
和![]() 为边在线段下方作正方形
为边在线段下方作正方形![]() 和正方形
和正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的面积之和等于正方形
的面积之和等于正方形![]() 和正方形
和正方形![]() 面积之和的两倍.
面积之和的两倍.
(1)请你画出正方形![]() 和正方形
和正方形![]() (不必尺规作图);
(不必尺规作图);
(2)设![]() ,
,![]() ,根据题意写出关于
,根据题意写出关于![]() 的等式并证明.
的等式并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
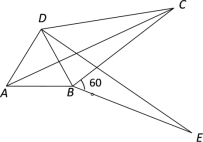
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边。
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称;
(2)如图,将![]() 绕顶点B顺时针方向旋转
绕顶点B顺时针方向旋转![]() ,得到
,得到![]() ,连接AD、DC,
,连接AD、DC,![]() ,求证:
,求证:![]() ,即四边形ABCD是勾股四边形。
,即四边形ABCD是勾股四边形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A1B1C1 | A1(﹣3,2) | B1(﹣1,b) | C1(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.
(1)求A,B,C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC,BC,若点E是线段AB上的一个动点(与点A,点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a, P为正方形边上一动点,运动路线是A-D-C-B-A,设P点经 过的路程为x,以点A,P,D为顶点的三角形的面积是y,图象反映了y与x的关系,当![]() 时,x=_____.
时,x=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com