Question

【题目】如图，在△ABC中，AB＝AC，E在线段AC上，D在AB的延长线，连DE交BC于F，过点E作EG⊥BC于G．

（1）若∠A＝50°，∠D＝30°，求∠GEF的度数；

（2）若BD＝CE，求证：FG＝BF+CG．

Answer 1

【答案】（1）55°；（2）见解析

【解析】

（1）根据等腰三角形两底角相等及三角形内角和定理求出∠C，再根据直角三角形两锐角互余求出∠CEG，然后根据三角形的外角的性质求出∠CEF，即可得到结论；

（2）过点E作EH∥AB交BC于H，根据平行线的性质可得∠ABC=∠EHC，∠D=∠FEH，然后求出∠EHC=∠C，再根据等角对等边可得EC=EH，得出BD=EH，再利用“角角边”证明△BDF和△HEF全等，根据全等三角形对应边相等可得BF=FH，根据等腰三角形三线合一的性质可得CG=HG，即可得到结论．

（1）∵∠A=50°，∴∠C（180°﹣∠A）（180°﹣50°）=65°．

∵EG⊥BC，∴∠CEG=90°﹣∠C=90°﹣65°=25°．

∵∠A=50°，∠D=30°，∴∠CEF=∠A+∠D=50°+30°=80°，∴∠GEF=∠CEF﹣∠CEG=80°﹣25°=55°；

（2）过点E作EH∥AB交BC于H，则∠ABC=∠EHC，∠D=∠FEH．

∵AB=AC，∴∠ABC=∠C，∴∠EHC=∠C，∴EC=EH．

∵BD=CE，∴BD=EH．

在△BDF和△HEF中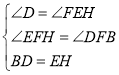，∵，∴△BDF≌△HEF（AAS），∴BF=FH．

又∵EC=EH，EG⊥BC，∴CG=HG，∴FG=FH+HG=BF+CG．